물리학 상식 : 만유인력과 케플러 법칙

여기서는 고전 중력 혹은 뉴턴 중력 (Newtonian gravity)이라고도 불리우는 만유인력의 개념과, 이로 인해 파생되는 행성의 궤도 운동인 케플러 (Kepler) 운동에 대해 알아봅시다. 고등학교 지구과학 교과서의 천문학 부분에 등장하는 3개의 케플러 법칙에 대해서도 살펴보겠습니다.

 

반응형

 

질량을 가진 물체들이 서로를 끌어당기는 힘이라고 볼 수 있는 만유인력은 등방성 (isotropy)을 가지고 있습니다. 다시 말해서 점으로 된 질량이 있을 때, 이로 인해 파생되는 중력장의 세기는 점 질량으로부터의 거리에 따라 달라지지만 방향에는 무관한 함수라는 것이죠. 그렇기 때문에 3차원 공간에서 행성의 궤도 운동을 기술하기 위해서는 구면 좌표계를 활용하는 것이 좋습니다. 구면 좌표계의 정의와 특징에 대한 더 자세한 내용은 다음 포스팅에 소개되어 있습니다.

 

수학 상식 : 원통 좌표계와 구면 좌표계

 

덧붙여 뉴턴의 운동 법칙은 물체의 위치와 속도를 시간에 대한 함수로 구하기 위한 연립 상미분 방정식의 형태를 띠고 있는데요. 미분과 미분 방정식의 개념이 생소하게 느껴지는 분들에게는 다음 포스팅이 큰 도움이 되리라 생각합니다.

 

수학 상식 : 미분과 적분 이해하기

 

만유인력

만유인력의 법칙 (law of universal gravitation)은 뉴턴이 1687년에 출판한 저서 프린키피아 (Principia)의 일부로서, 질량을 가진 두 물체 사이에 끌어당기는 힘에 대한 것입니다. 점의 형태를 가진 두 개의 물체가 있을 때, 서로에게 작용하는 인력의 크기와 방향이 질량과 거리에 따라 어떻게 달라지는지를 구체적으로 정의하고 있는데요.

 

• 힘의 크기는 두 물체의 질량의 곱에 비례합니다.
• 힘의 크기는 두 물체 간의 거리의 제곱에 반비례합니다.
• 각 물체에 가해지는 인력의 방향은 정확하게 상대방 물체로 향하는 방향과 같습니다.
• 작용-반작용의 법칙에 따라, 두 물체가 각각 받는 힘은 크기가 동일하고 방향이 반대입니다.

 

벡터의 개념을 동원하여 이를 나타내면 다음과 같습니다.

 

 

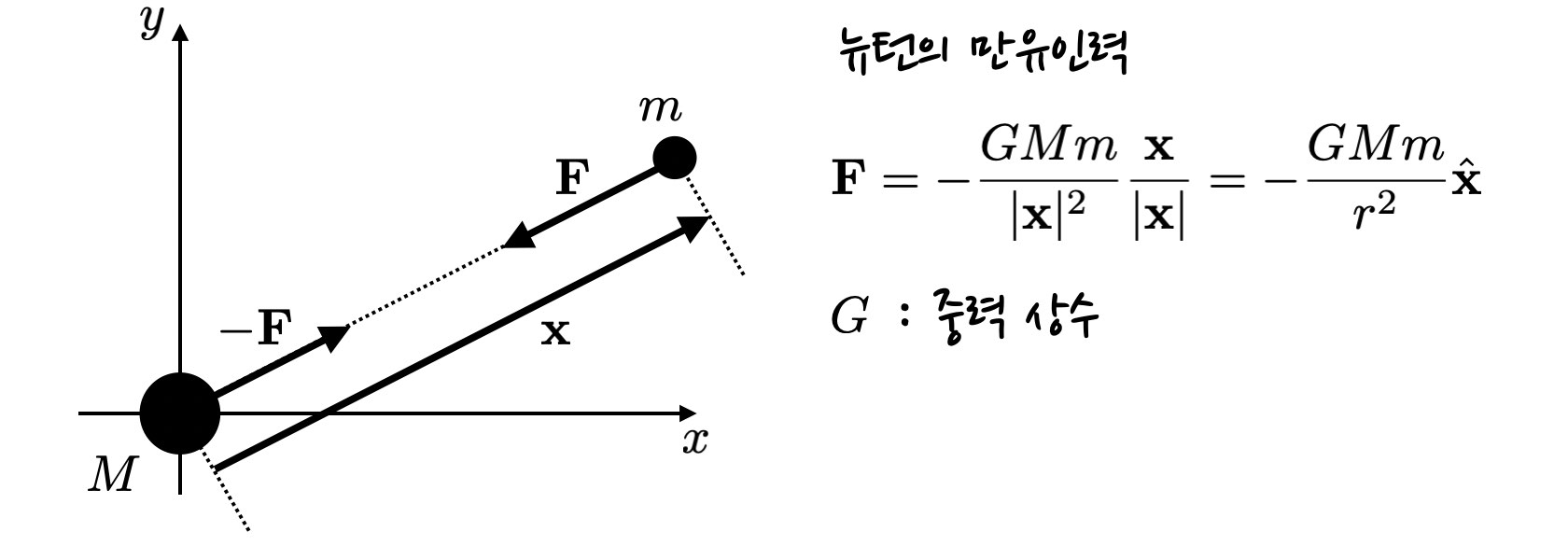
만유인력의 세기와 방향을 질량과 변위 벡터에 대한 함수로 나타낼 수 있고, 여기서 중력 상수가 들어갑니다. 참고로 고차원 공간 내의 방향성을 가진 벡터는 볼드체를 사용하거나 알파벳 위에 화살표를 붙여서 표기하는 것이 일반적입니다.

 

뉴턴의 운동 법칙과 만유인력을 연계해서, 태양 주위를 공전하는 행성의 운동에 대해 알아볼 수 있습니다. 다시 말해서 행성의 가속도가 만유인력에 의해 결정되는 미분방정식을 풀게 되면, 행성의 위치와 속도가 시간에 따라 어떻게 변화하는지를 알 수 있게 되죠. 행성의 궤도가 놓인 평면을 x-y 평면으로 상정하고, 태양을 그 중심에 놓습니다. 그러면 행성과 태양 간의 직선거리와 x축으로부터 벌어진 각도를 시간에 대한 함수로 구할 수 있게 됩니다.

 

 

한가지 짚고 넘어갈 점이 있다면 태양 역시 행성으로부터 만유인력을 받는다는 점입니다. 즉 작용-반작용의 법칙에 따라 행성을 향해 끌려들어가는 힘이 존재하기 때문에, 원칙적으로는 궤도 운동을 하게 되는데요. 하지만 태양의 질량은 태양계 행성들의 질량을 모두 더한 것보다도 훨씬 크기 때문에, 태양의 위치는 고정되어 있다고 가정해도 무리가 없다고 하겠습니다.

 

케플러 법칙

케플러 행성운동법칙 (Kepler's laws for planetary motion)은 태양 주위를 공전하는 행성들의 궤도 운동을 설명하기 위한 법칙인데요. 17세기 초에 이를 발표한 독일의 수학자이자 천문학자인 요하네스 케플러 (Johannes Kepler)에게서 그 이름을 따왔습니다.

 

역사적으로는 만유인력의 개념이 등장하기 이전에, 티코 브라헤의 관측결과를 바탕으로 정립되었습니다. 케플러 사후 뉴턴이 태양과 행성 간의 만유인력으로부터 케플러 법칙이 파생된다는것을 증명함으로써, 고전 역학의 일부로 편입되었고 오늘날에는 교과서에도 박제되어 있습니다.

 

 

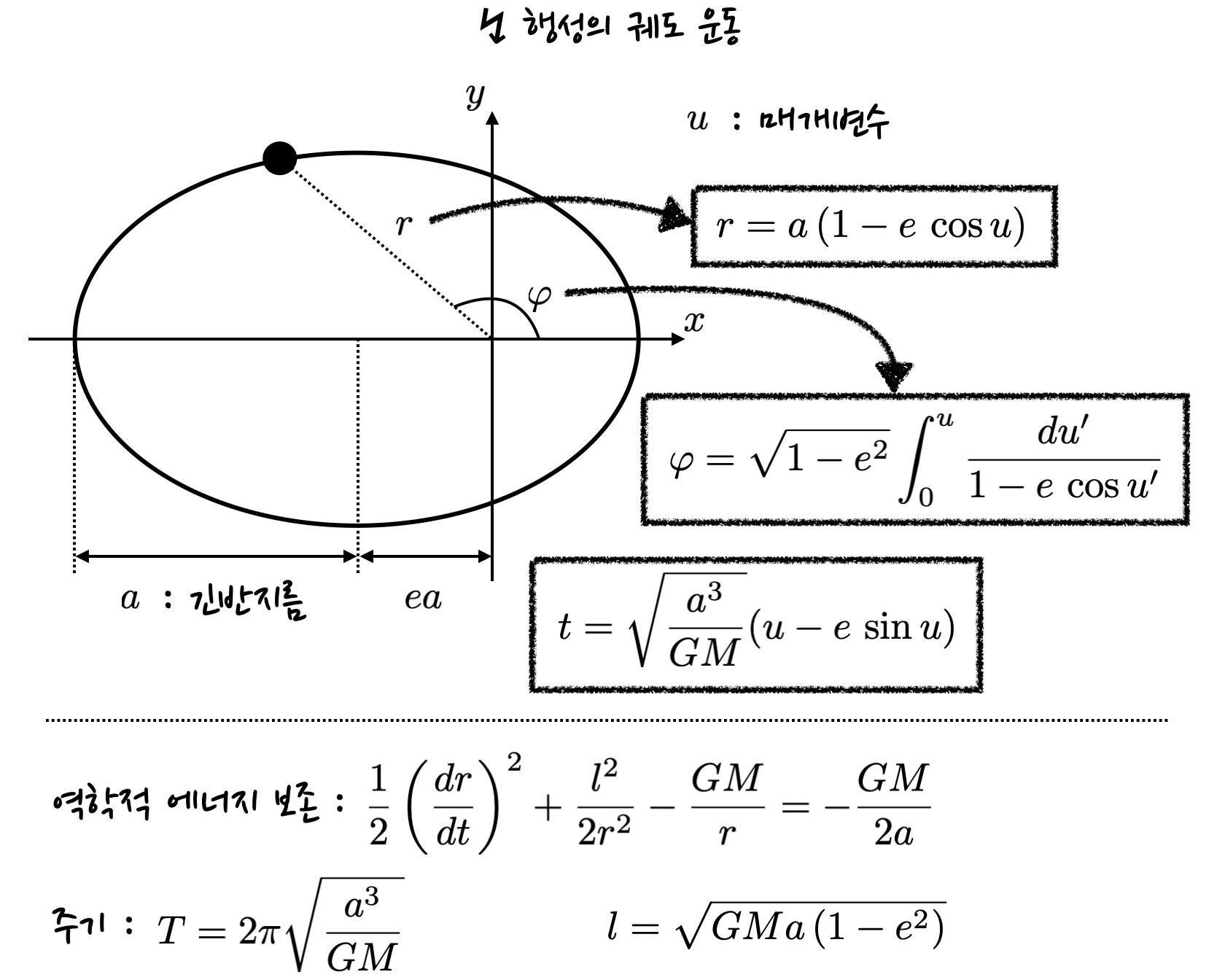
1. 타원 궤도의 법칙

케플러 제 1 법칙은 만유인력의 영향으로 태양 주위를 공전하는 행성들이 어떤 형태의 궤도를 따르는지에 대한 것입니다. 타원 궤도의 법칙에 따르면, 행성의 공전 궤도는 타원 (ellipse)의 형태를 띠고 있고 태양이 초점 중의 하나에 위치해 있습니다. 타원의 정의에 대해 간단히 말하자면, 서로 떨어진 두 초점으로부터의 거리의 합이 일정한 점들의 집합이라고 할 수 있는데요. 두 초점의 위치가 동일한 경우, 원이 됩니다.

 

타원을 정의하는 주요 개념으로는 긴반지름 (semi-major axis), 짧은반지름 (semi-minor axis) 및 초점이 중심으로부터 얼마나 벗어나 있는지를 수치화한 이심률 (eccentricity)이 있습니다. 이번 포스팅에서는 긴반지름과 이심률을 알파벳 소문자 a와 e로 각각 표기했습니다.

 

2. 면적 속도 일정의 법칙

태양과 행성 간의 직선을 상정한 뒤, 행성이 공전함에 따라 이 직선이 휩쓸고 지나가는 면적을 생각해 볼 수 있습니다. 단위 시간 동안 얼마나 넓은 면적을 휩쓸고 지나가는지에 대해서도 살펴볼 수 있는데, 이것이 바로 면적속도의 개념입니다. 케플러 제 2 법칙은 이러한 면적속도가 항상 일정하다는 것으로, 행성이 태양에 가까이 접근할수록 공전 속도가 빨라진다는 점을 시사하고 있습니다.

 

면적 속도라는 것은 기하학적인 개념이지만, 면적 속도 일정의 법칙은 물리적으로 행성의 각운동량 보존과 관련이 있습니다. 물체의 직진 혹은 병진 운동에 의해 운동량이 생긴다면, 각운동량은 물체의 회전이나 공전으로 인해 발생하는 물리량인데요. 행성을 끌어들이는 중력의 방향이 정확하게 태양 쪽을 가리키기 때문에, 태양의 중력만 가지고는 행성의 평균적인 공전 속력을 늦추거나 가속시킬 수 없는 것입니다.

 

 

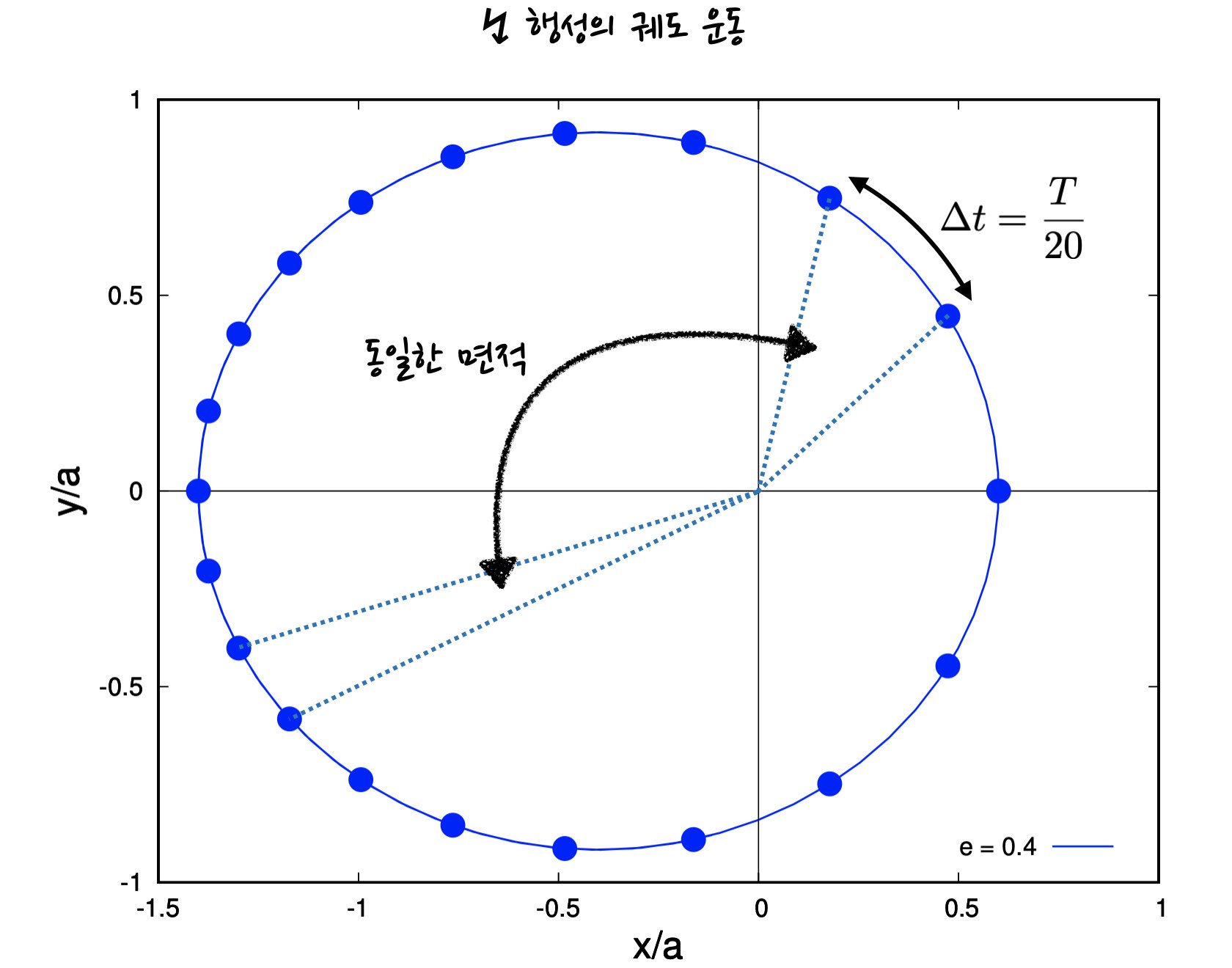
일정한 시간 간격을 두고 행성의 위치가 어떻게 달라지는지를 살펴보면, 태양이 있는 중심으로부터 멀리 떨어져 있을수록 공전 속도가 느려진다는 것을 알 수 있습니다.

 

3. 조화의 법칙

케플러 제 3 법칙인 조화의 법칙은 타원 궤도의 긴반지름의 길이와 공전 주기 간의 관계를 정의하고 있습니다. 타원 궤도 긴반지름의 세제곱이 주기의 제곱에 비례한다는 것인데요. 이는 앞서 구했던 케플러 운동의 해로부터 유도할 수 있습니다.

 

좀 더 자세하게 이야기하자면, 행성 궤도의 긴반지름, 공전 주기와 태양의 질량 3개 요소 간의 관계라고도 볼 수 있습니다. 3개 중의 2개를 알면 나머지 하나를 특정할 수 있게 되는 거죠. 예를 들어서 태양의 질량과 행성의 공전주기를 알고 있으면 케플러 제 3 법칙을 통해 그 행성의 궤도 긴반지름을 알아낼 수 있는 것입니다.

 

이러한 특징 때문에 쌍성계의 질량을 알아내는데에도 케플러 제 3 법칙이 사용되는데요. 쌍성계란 간단히 말해서 2개의 별이 중력에 이끌려 서로를 공전하는 것이라 할 수 있습니다. 쌍성계의 공전 주기와 궤도 긴반지름을 측정한 뒤, 이들을 가지고 질량을 유추해내는 방법이 사용됩니다. 실제 우주에 있는 별들 다수는 쌍성계를 이루고 있기 때문에, 상당히 실용적이라고 볼 수 있습니다.

 

---

 

앞에서 언급한 조화의 법칙에 대해서 좀 더 엄밀하게 말하자면, 공전하는 두 천체의 질량의 합이 궤도 긴반지름의 세제곱에 비례하고 공전 주기의 제곱에 반비례한다는 것입니다. 이를 좀 더 자세하게 이해하기 위해서는 무게중심과 환산질량 (reduced mass)의 개념을 도입해서 이체 (two-body)문제를 재구성할 필요가 있는데요. 여기에 대해서는 다음 포스팅에 더 자세한 내용이 소개되어 있습니다.

 

물리학 상식 : 이체 문제의 환산 질량

 

면적 속도가 일정하다는 것은 각운동량이라는 물리량이 보존된다는 의미를 가지고 있다고 앞에서 이야기했습니다. 각운동량은 물체의 회전이나 공전 운동이 가지는 임팩트를 수치화하기 위한 개념이죠. 각운동량의 정의와 특징에 대한 더 자세한 내용은 다음 포스팅에 소개되어 있습니다.

 

물리학 상식 : 에너지, 운동량과 각운동량

 

행성이 태양 주위를 공전하는 이유는 태양으로부터의 중력이 구심력으로 작용하기 때문이라고도 볼 수 있습니다. 구심력은 물체의 운동 방향을 바꾸는 힘으로서, 운동 방향에 수직으로 작용하는 것이 특징입니다. 구심력과 원심력의 정의와 특징에 대해서는 다음 포스팅에 더 자세하게 소개되어 있습니다.

 

물리학 상식 : 원심력과 구심력