수학 상식 : 미분과 적분 이해하기

이번 포스팅에서는 고등학교 수학의 종착역이자 고급 수학의 출발점이라고 할 수 있는 미분과 적분에 대해 알아보도록 합시다. 미분과 적분의 기본 개념뿐만 아니라, 미분방정식이나 적분변환 등의 확장된 개념들에 대해서도 짚어보도록 하겠습니다.

 

반응형

 

미분

개념

미분 (derivative)은 주어진 함수가 매개변수 또는 인자의 값에 따라 얼마나 빠르게 변화하는지를 수치화한 것입니다. 다시 말해서 인자의 값을 아주 약간 바꿨을 때, 함수의 값이 변하는 비율을 나타낸 것인데요. 기하학적으로 보면, 이는 함수를 그래프로 그렸을 때의 기울기에 해당합니다. 미분으로 주어진 함수를 도함수라는 명칭으로 부르기도 합니다. 예컨대 매개변수 x 에 대한 함수 f(x) 를 x에 대해 미분하여 얻은 함수를 f의 도함수라고 부르고, df/dx 라는 분수식으로 쓰거나 프라임을 붙여서 f' 으로 표기하는 식입니다.

 

함수의 값이 무한대로 발산하거나 기울기가 불연속적으로 변하지 않는 이상, 함수를 반복적으로 미분하는 것이 가능한데요. 도함수를 다시 미분하면, 이는 함수를 2번 미분한 것으로 2차 미분 또는 2계 미분이라고 부릅니다. 이를 일반화해서 함수를 N번 미분한 것을 N차 미분이라고 부릅니다.

 

 

미분과 관련해서 알아두면 좋은 몇가지 특징이 있습니다. 두 개의 함수를 곱한 함수의 미분이 어떻게 주어지는지, 그리고 합성함수의 미분을 구하기 위한 연쇄 법칙 (chain rule)에 대해서도 알고 있으면 유용하죠. 특히 연쇄 법칙은 역함수의 미분을 이해하는데 있어서 필수요소라고 할 수 있습니다.

 

 

물리학에서 물체의 운동을 수치화하기 위한 개념인 속도를 정의하는데 있어서 미분이 들어갑니다. 정확히 말하자면, 물체의 위치 벡터를 시간에 대해 미분한 것이 속도 벡터가 되죠. 그리고 이로부터 에너지, 운동량 및 각운동량을 구하면 물체의 운동이 가진 임팩트를 수치화할 수 있게 되는데요. 여기에 대한 더 자세한 내용은 다음 포스팅에 소개되어 있습니다.

 

물리학 상식 : 에너지, 운동량과 각운동량

 

상미분 vs 편미분

단일한 매개변수를 받는 함수의 미분을 상미분 (ordinary derivative)이라고 부르는 반면에, 여러 개의 매개변수를 받는 다변수 함수의 경우 편미분 (partial derivative)을 다룰 필요가 있습니다. 편미분의 개념에 대해 간단히 말하자면, 다른 변수들의 값을 일정하게 유지하면서, 특정한 하나의 변수에 대해서만 그 값을 살짝 바꿔서 미분을 수행하는 것입니다.

 

미분방정식

앞에서 미분의 개념에 대해 살펴보았으니, 이제는 미분방정식 (differential equation)에 대해 알아봅시다. 미분방정식이란, 정보를 알아내고자 하는 함수들의 미분 사이의 관계를 규정한 방정식을 말합니다. 미분방정식을 풀거나 해를 구한다는 말은, 미분이 특정한 조건을 만족하는 함수의 형태를 알아내는 것과 같다고도 할 수 있죠. 예를 들어서 미분이 본래의 함수에 비례한다는 조건을 걸게 되면, 이것 역시 미분 방정식이라고 할 수 있으며, 그 해는 지수함수로 주어집니다.

 

이공계 분야의 직업에 종사하는 분이라면 이 미분방정식을 피해가는 것이 불가능할 정도로 과학 및 공학 분야에서 흔하게 등장하는 수학적 개념입니다. 물리학에서 자연현상을 기술하는 법칙이나 모형이 특정한 미분방정식을 상정하고 있는 경우가 매우 많죠. 뉴턴의 고전역학만 봐도 어떤 물체의 위치 변화율은 속도에 의해 결정되고, 속도의 시간 변화율인 가속도는 물체에 가해지는 힘 (외력)에 의해 결정되는 미분 방정식의 형태를 띠고 있습니다. 미분 방정식의 또 다른 예시로는 파동 방정식이 있으며, 이는 매질의 변위를 시간과 공간에 대한 함수로 구하기 위한 편미분 방정식입니다.

 

 

한가지 더 짚고 넘어가자면, 미분방정식의 해를 특정하기 위해서는 미분과 관련된 조건식 뿐만 아니라, 특정 지점에서 함수들의 값을 지정해줄 필요가 있습니다. 미분을 통해서 함수의 기울기는 알 수 있지만, 함수의 절대적인 값은 알 수 없기 때문이죠.

 

뉴턴 역학을 따르는 가장 간단한 예시 중 하나로 진자운동이 있습니다. 천장에 매달린 진자는 중력이 복원력으로 작용하는 왕복운동을 한다고 볼 수 있는데요. 이러한 진자의 위치 및 속력이 시간에 따라 어떻게 변하는지를 알아내기 위해서는 미분방정식을 풀어야 합니다. 더 자세한 내용은 다음 포스팅에 소개되어 있습니다.

 

C/C++ Runge-Kutta 방법으로 알아보는 진자운동

 

태양의 중력에 의해 공전 운동을 하는 행성을 기술하기 위한 방정식 역시 뉴턴 운동 법칙에 따른 미분방정식입니다. 이 방정식의 해를 구하면, 케플러 법칙 등을 비롯해서 공전 운동의 여러 특징들을 이해할 수 있게 되는데요. 더 자세한 내용이 궁금하시다면 다음 포스팅을 읽어보는 것도 좋습니다.

 

물리학 상식 : 만유인력과 케플러 법칙

 

구면처럼 휘어져 있는 공간에 있는 두 점 사이의 최단 경로를 알아내기 위한 지름길 (geodesic) 방정식 역시 미분방정식의 형태를 띠고 있습니다. 예를 들어서 항공기가 출발지와 목적지 사이의 최단 경로를 따라 비행할 때, 위도 및 경도가 시간에 따라 어떻게 변하는지를 알아내기 위해서는 경계조건과 함께 미분방정식을 풀어야 합니다. 다음 포스팅에 더 자세한 내용이 소개되어 있습니다.

 

C/C++ 반복-이완 계산법으로 알아보는 비행경로

 

자유롭게 흐를 수 있는 유체에서는 압력이 높은 곳에서 낮은 곳으로 유체를 밀어내는 힘이 발생합니다. 그런데 만일 압력의 차이에 의한 힘과 외부에서 가해지는 힘이 상쇄되어 알짜힘이 0이 된다면, 유체의 운동 상태가 일정한 평형상태가 되겠죠. 이러한 정역학적 평형상태를 나타내는데 있어서 미분방정식이 등장합니다. 여기에 대한 더 자세한 사항은 다음 포스팅에 소개되어 있습니다.

 

물리학 상식 : 유체의 정역학적 평형

 

적분

부정적분

부정적분은 간단히 말해서 미분의 역연산이라고 볼 수 있습니다. 이말인즉슨 주어진 함수를 부정적분한 함수를 다시 미분하면, 본래의 함수로 되돌아온다는 뜻이죠. 한 가지 짚고 넘어갈 점이 있다면, 부정적분에 상수를 더한 함수 역시 부정적분된 함수라는 것인데요. 상수를 미분하면 0이 되기 때문입니다.

 

정적분

리만 적분 (Riemann integration)이라고도 불리우는 정적분은 정의역 내에서 특정한 범위를 상정하고, 함수를 인자로 받은 뒤 숫자를 내놓는 연산 중의 하나입니다. 정의역을 가로축 x로 나타내고 함수의 값을 세로축 y로 나타냈을 때, 정적분의 기하학적 의미는 함수가 나타내는 곡선과 x축 사이의 넓이와도 같습니다.

 

 

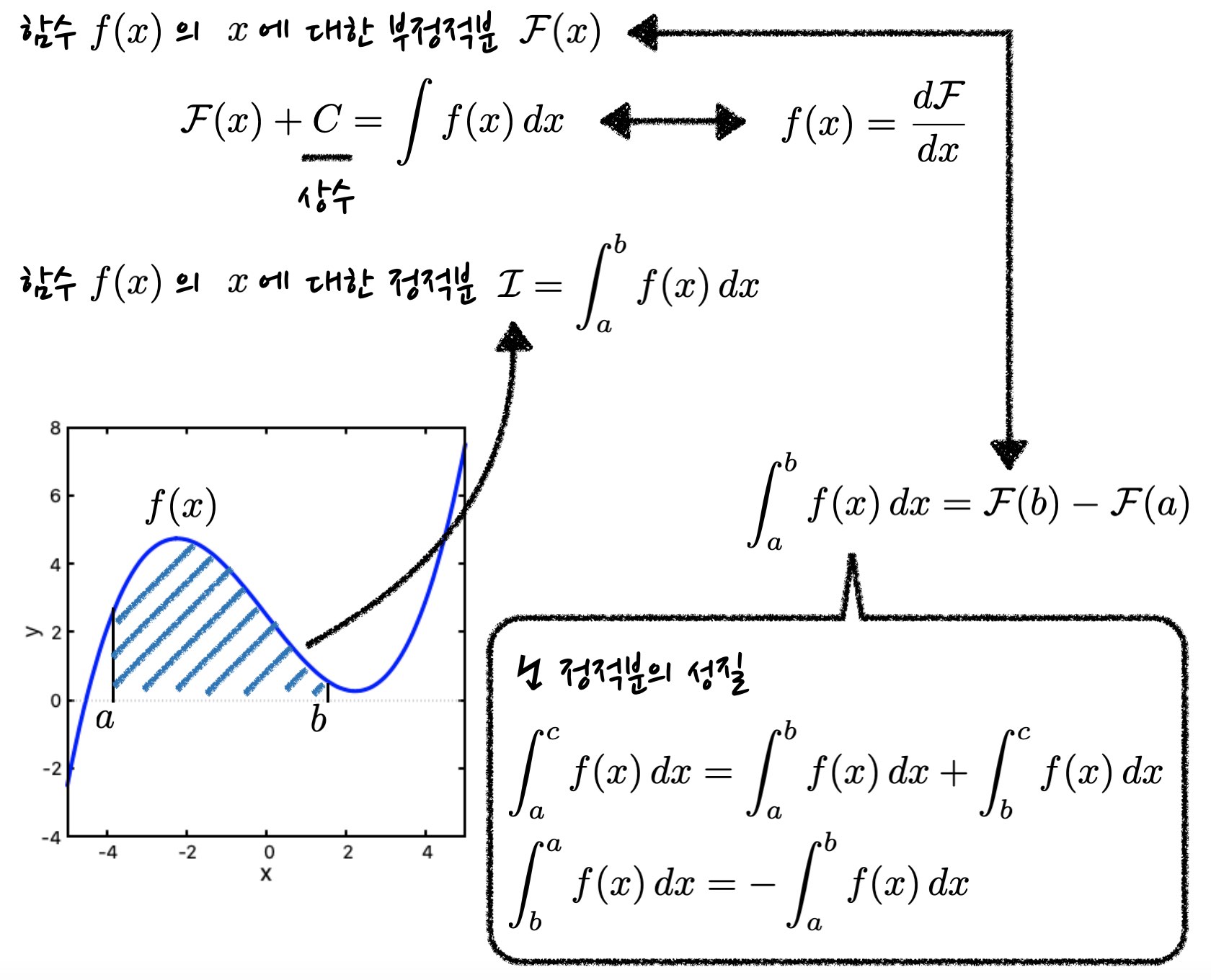
정적분이 가지는 기하학적 의미로부터, 정적분이 가지는 특징들 및 부정적분과의 관계도 도출해낼 수 있습니다.

 

뿐만 아니라 함수를 벡터로 간주하고, 이들의 내적을 정의하는데 있어서도 정적분이 사용됩니다. 벡터로서의 함수가 정의되는 힐베르트 공간에 대한 더 자세한 사항은 다음 포스팅에 소개되어 있습니다.

 

수학 상식 : 벡터의 덧셈과 곱셈 (내적, 외적)

 

정적분을 통해서 물리법칙을 정의할 수도 있는데요. 이를 라그랑지안 역학이라고 부르며, 변분법이라고 불리는 방법을 통해 미분방정식을 도출해낼 수 있습니다. 다음 포스팅에 더 자세한 내용이 소개되어 있습니다.

 

수학 상식 : 변분법과 라그랑지안 역학

 

확률밀도함수를 통해서 여러 자연현상이나 사회현상들을 통계적으로 다루는 데 있어서도 정적분이 사용됩니다. 확률밀도함수는 연속적인 값을 가질 수 있는 변수의 확률 분포를 정의한 함수인데요. 더 자세한 내용이 궁금하신 분들에게는 다음 포스팅이 큰 도움이 되리라 생각합니다.

 

수학 상식 : 확률 분포와 확률밀도함수

 

적분 대상이 되는 함수가 복잡한 형태를 띠고 있으면, 컴퓨터를 이용해서 정적분의 값을 구하는 것이 해결책이 될 수 있습니다. 대표적인 방법으로서, 적분 구간을 여러개로 나누고 함수의 형태에 따라 결정되는 여러개의 사다리꼴의 면적을 구하는 것이 있습니다. 이를 사다리꼴 공식 (trapezoidal rule)이라고 부르며, C/C++ 프로그램에서 구현하는 방법과 함께 다음 포스팅에 더 자세하게 소개되어 있습니다.

 

사다리꼴 공식을 이용한 C/C++ 수치 적분

 

적분변환

주어진 함수에다가 핵 (kernel) 함수를 곱한 뒤, 이를 적분하여 다른 변수를 인자로 하는 함수로 변환하는 것을 적분변환이라고 하는데요. 좀 더 자세히 말해서 x라는 변수를 인자로 받는 함수가 있고, x와 s라는 변수를 가진 핵 함수를 곱해서 x에 대해 정적분을 하게 되면, 그 결과로 나오는 함수는 s의 값에 따라 달라지겠죠. 이렇게 나온 s에 대한 함수가 바로 적분변환의 결과라고 할 수 있습니다.

 

 

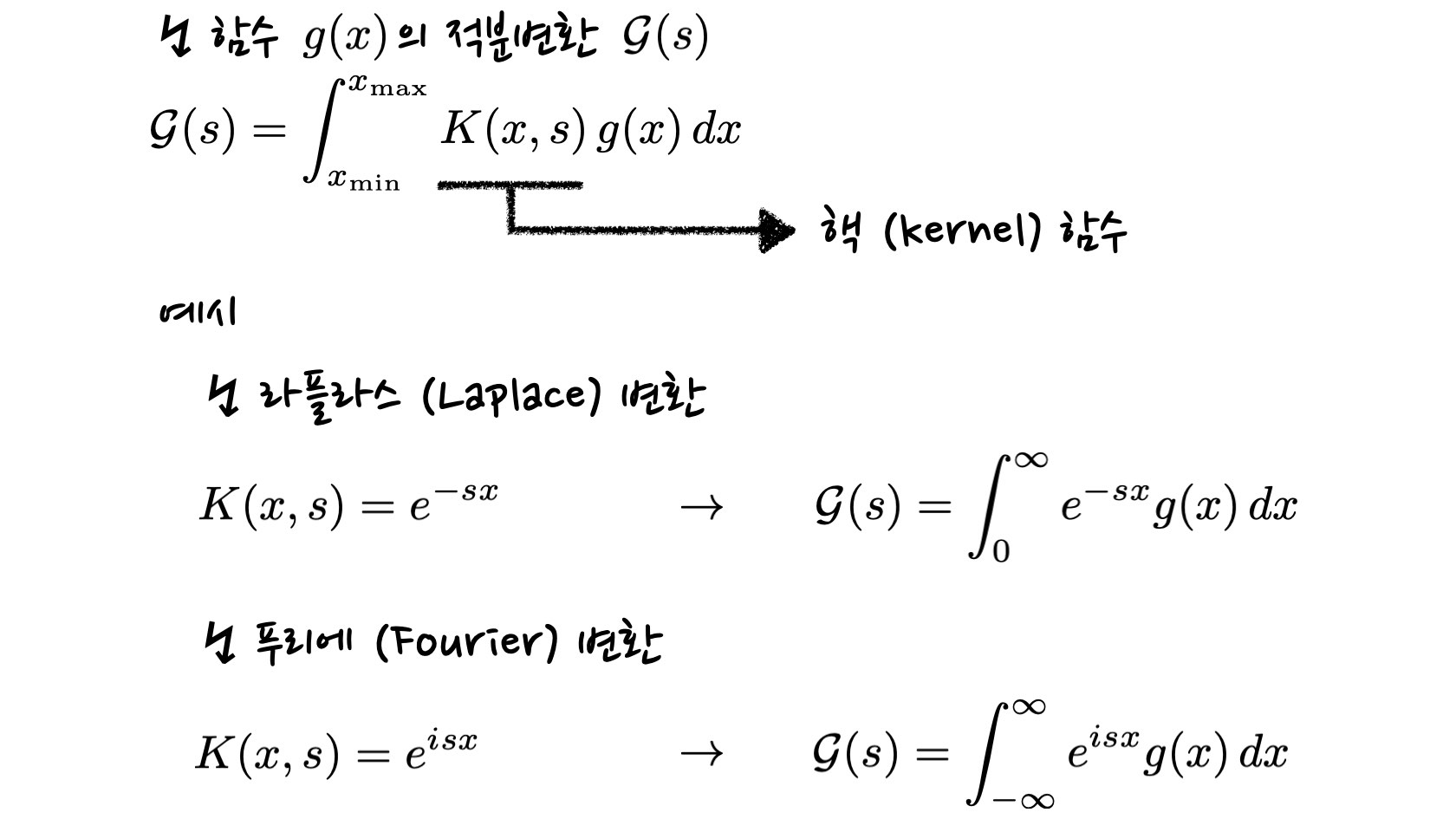
이공계 분야에서 실무적으로 많이 사용되는 적분변환으로는 라플라스 변환과 푸리에 변환이 있는데요. 이들은 앞서 언급한 미분방정식을 푸는데에 유용하게 쓰입니다. 예를 들어서 시간에 대한 미분방정식이 주어졌을 때, 푸리에 변환을 통해 주파수에 대한 방정식으로 바꿔서 해를 구한 뒤, 다시 푸리에 역변환을 통해 시간에 대한 함수로 해를 구하는 방식이 있습니다.

 

앞서 언급한 미분방정식과 함께 적분변환의 개념에 친숙해지고 나면 여러가지 물리 현상들을 더 깊이있게 이해해 볼 수 있습니다. 파동 현상도 그 중 하나인데요. 파동을 구성하는 요소들에 대한 더 자세한 내용은 다음 포스팅에 소개되어 있습니다.

 

물리학 상식 : 파동의 기본개념

 

위에서 예로 든 푸리에 변환의 경우 기본적으로 적분변환입니다만, 불연속적인 격자 공간에서 진행되는 이산 푸리에 변환의 경우 컴퓨터를 이용한 수치해석에서 흔하게 사용됩니다. C언어나 C++ 프로그램에서 이러한 고속 푸리에 변환을 수행하기 위한 라이브러리 중 하나로는 FFTW가 있으며, 다음 포스팅에 더 자세히 소개되어 있습니다.

 

FFTW : C/C++ 고속 푸리에 변환 라이브러리

 

---

 

같이 알고 있으면 좋은 수학 지식

 

원주율과 삼각함수

수학 상식 : 원주율과 삼각함수

 

지수함수와 로그함수

수학 상식 : 지수함수와 로그함수

 

테일러 급수 전개

수학 상식 : 테일러 급수 전개