물리학 상식 : 에너지, 운동량과 각운동량

여기서는 물체의 운동을 수치화하는데 있어서 중요한 물리량들인 에너지 (energy), 운동량 (momentum) 및 각운동량 (angular momentum)에 대해 알아보도록 합시다. 이들은 고등학교 물리 교과과정에서부터 등장하는 기초적인 내용들이지만, 대학교 및 대학원을 거쳐서 연구를 하는 동안에도 지속적으로 접하는 중요한 개념들입니다.

 

반응형

 

뉴턴의 고전역학에서 이들이 어떻게 정의되며, 어떠한 특징들이 있는지를 알아봅시다. 물체의 이동 속도가 빛의 속도에 근접하는 상황에서 에너지와 운동량의 정의가 어떻게 확장되는지도 살펴보겠습니다. 이를 위해서는 벡터들의 곱셈 연산인 내적과 외적에 대해 알아둘 필요가 있습니다. 이들이 생소하게 느껴지는 분들은 시작하기에 앞서서 다음 포스팅을 읽어보시면 큰 도움이 되리라 생각합니다.

 

수학 상식 : 벡터의 덧셈과 곱셈 (내적, 외적)

 

운동량과 운동에너지를 정의하는데 있어서, 시간과 공간에 대한 변화율인 미분에 대해 언급을 하게 될텐데요. 미분의 정의와 특징에 대해서는 다음 포스팅에 더 자세한 내용이 소개되어 있습니다.

 

수학 상식 : 미분과 적분 이해하기

 

에너지와 운동량

뉴턴역학에서의 정의와 특징

먼저 물체의 직진 혹은 병진 운동에 의해 발생하는 물리량인 운동량과 운동 에너지에 대해 알아봅시다. 이들은 직진운동을 하는 물체가 가진 임팩트를 수치화한 개념이라고 볼 수 있습니다.

 

예를 들어서 2층 창문에서 떨어진 어떤 물체가 머리에 맞는 상황을 상정해 봅시다. 탁구공에 맞을 때는 간지러운 정도로 끝나겠지만, 사과에 맞으면 꽤나 아프겠죠. 그리고 2층에 정지해 있다가 떨어진 경우에 비해서, 누가 우리를 노리고 빠르게 던진 경우에 더 아플 겁니다. 또 다른 예시로서 총을 발사하는 경우에도, 총알 자체는 별로 무겁지 않지만 날아가는 속도가 워낙 빠르기 때문에 나무판자 정도는 무리없이 뚫어버립니다.

 

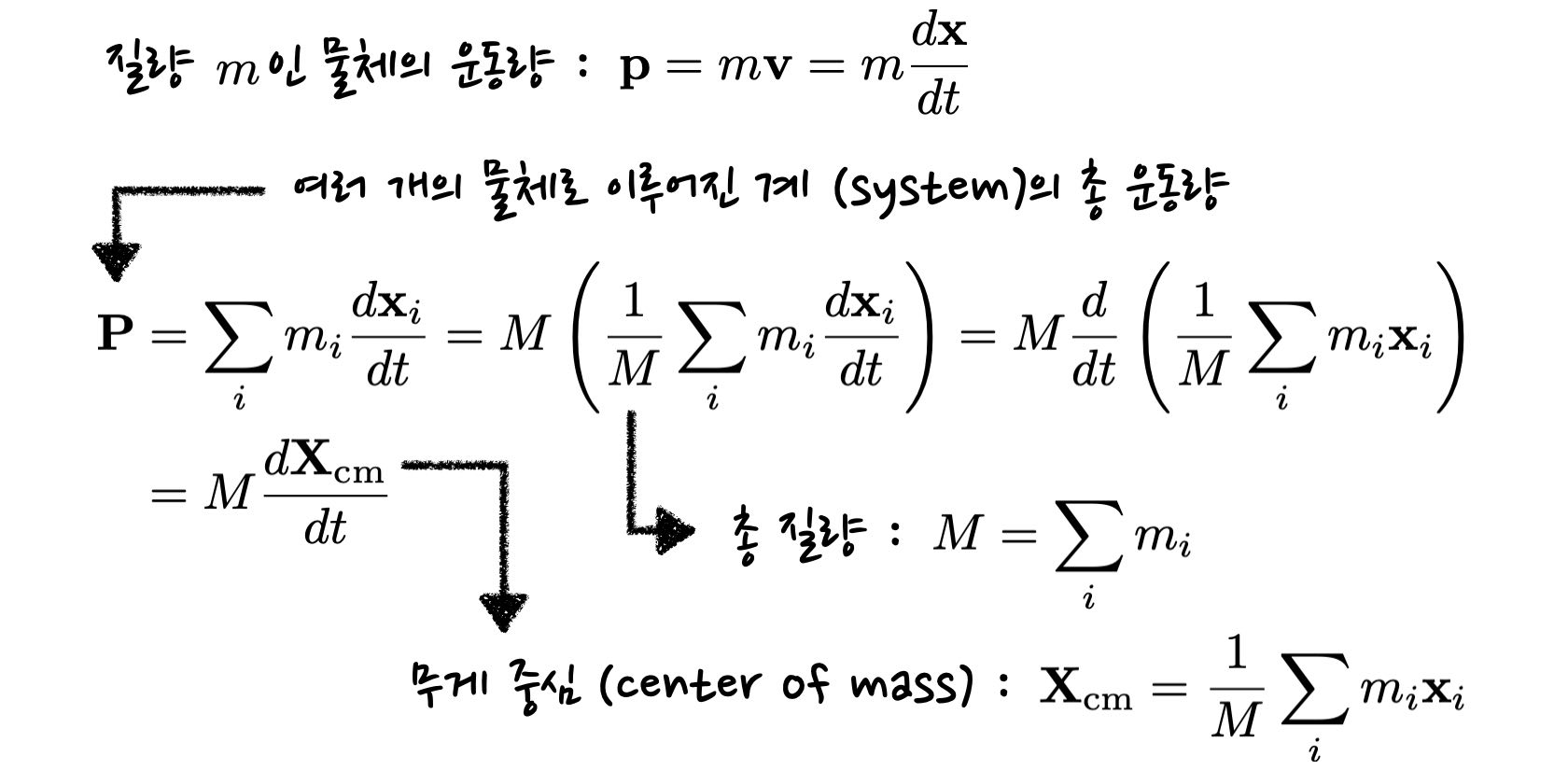
뉴턴역학에서 물체가 가진 운동량은 이러한 경험을 수학적으로 체계화한 것으로 볼 수 있는데요. 이는 물체의 속도에 질량을 곱한 것으로 정의됩니다. 속도는 방향을 가지고 있는 벡터량이고 질량은 숫자이므로, 운동량 역시 벡터량이라는 것도 알 수 있습니다. 물체가 무겁고 빠를수록 그로 인한 파급력은 커지게 되는 셈이죠.

 

여러 개의 물체로 이루어진 집합 혹은 계 (system)가 있고, 외부에서 힘이 가해지지 않는 상황에서 운동량은 보존이 됩니다. 집합에 소속된 물체들 사이의 상호작용으로 인해 각 물체가 가진 운동량은 변할 수 있겠지만, 모든 물체의 운동량을 합친 총량은 시간이 지나도 변하지 않게 됩니다. 물론 외부에서 힘을 가하게 되면 그에 따라 총 운동량이 변하게 되겠지만요.

 

추가로 운동량을 통해서 무게중심 (center of mass)을 정의할 수 있습니다. 여러 개의 물체로 이루어진 계를 한 지점에 뭉뚱그렸을 때의 점질량 (point mass)을 상정한 뒤, 이 점질량이 가지는 운동량이 총 운동량이 된다는 조건을 생각해 볼 수 있는데요. 이러한 조건을 만족시키는 점질량의 위치가 바로 무게중심이 된다고 할 수 있습니다.

 

 

뉴턴의 운동법칙 중 2번째인 가속도의 법칙을 운동량을 가지고 표현을 하자면, 운동량의 시간 변화율은 물체에 작용한 힘과 같다고 할 수 있습니다. 질량이 일정하다면 운동량의 시간 변화율은 질량과 가속도의 곱으로 주어지기 때문입니다. 여기서 운동에너지와 위치에너지의 개념을 도출해볼 수 있습니다.

 

 

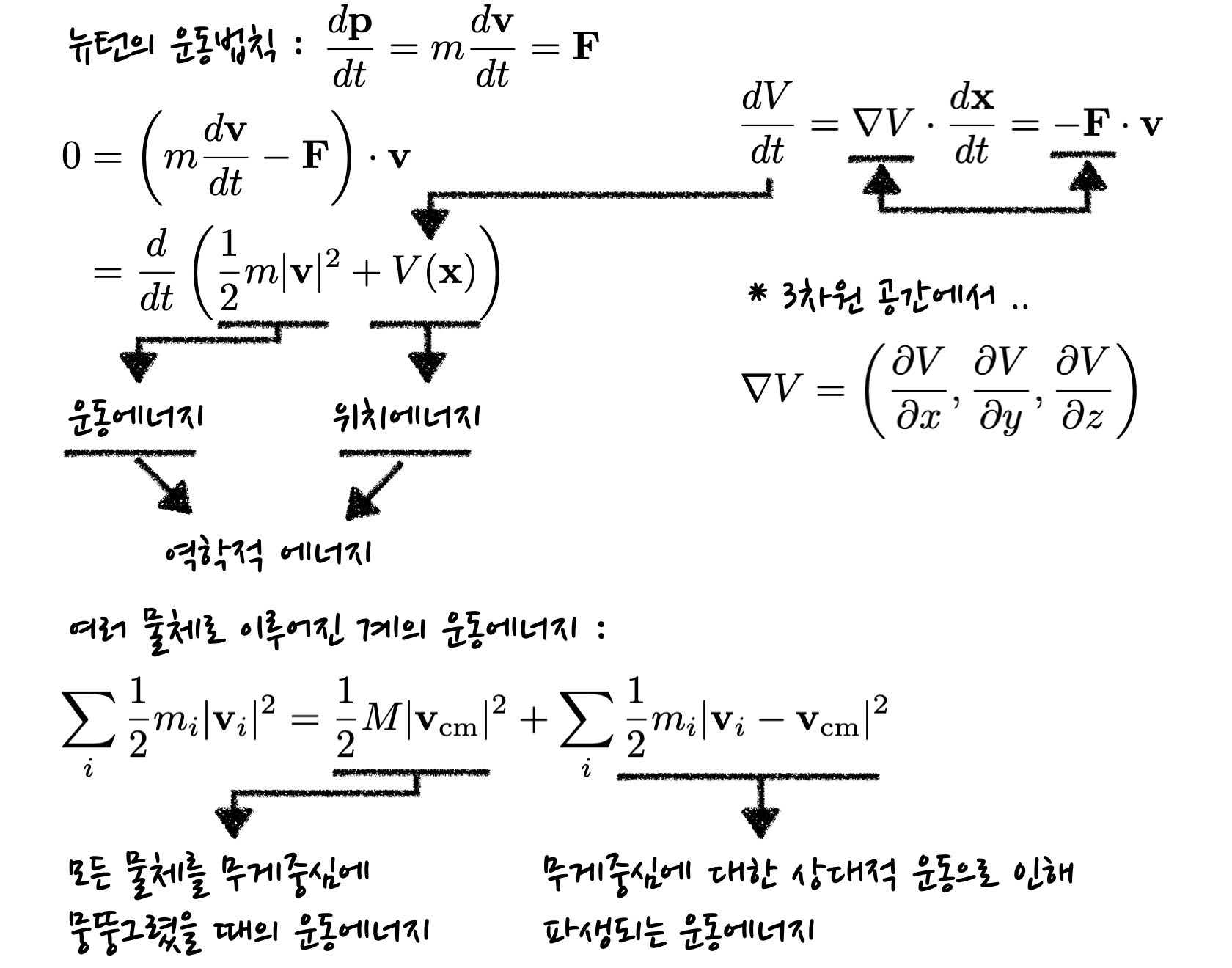
물체에 가해지는 힘이 스칼라 위치에너지 (scalar potential)의 미분으로 주어지는 형태를 상정하면, 역학적 에너지 보존이 성립하게 됩니다. 이말인 즉슨 운동에너지와 위치에너지의 합이 일정하게 된다는 뜻이 되겠습니다.

 

한가지 더 짚고 넘어갈 점은 여러 개의 물체로 이루어진 계의 운동에너지가 어떻게 나타나느냐에 대한 것인데요. 이는 물론 각 물체가 가진 운동에너지를 전부 더한 것입니다만, 이를 단순화할 수 있는 방법이 있습니다. 총 운동에너지는 모든 물체를 무게중심의 위치에 뭉뚱그렸을 때의 점질량이 가지는 운동에너지에다가 각 물체가 무게중심으로부터의 상대적인 운동에 따라 가지는 운동에너지를 합친 것이라는 점을 유추할 수 있습니다.

 

이러한 개념은 강체 (rigid body)가 포함된 문제를 다루는데 있어서 유용하게 사용됩니다. 예를 들자면 당구공이 굴러가는 상황에서는 당구공의 중심이 이동하는 것에서 파생되는 운동에너지와 당구공의 회전운동에 의해 생기는 운동에너지가 존재하죠. 이들을 별도로 계산한 뒤에 더하면, 그 당구공의 운동에너지를 구할 수 있게 되는 것입니다.

 

특수상대론에서의 확장

앞에서 언급한 뉴턴역학은 물체들의 속력이 빛의 속도에 비해 매우 작은 경우에 한해서 성립한다고 볼 수 있습니다. 물체의 속력이 빛의 속도에 비해 무시하지 못할 정도로 빠르다면, 에너지와 운동량의 개념을 그에 걸맞게 일반화할 필요가 있습니다.

 

 

뉴턴역학에서 정의되는 운동에너지는 스칼라량이고, 운동량은 벡터량이라고 앞에서 언급했는데요. 특수상대론에서는 에너지-운동량 4차원 벡터 (energy-momentum 4-vector)라는 개념이 등장합니다. 1차원 시간과 3차원 공간이 합쳐진 4차원 시공간에서 에너지를 시간 방향의 성분으로 하고, 3차원 벡터인 운동량을 공간 방향의 성분으로 하는 벡터입니다. 에너지와 운동량의 보존을 수학적으로 표현하면, 에너지-운동량 4차원 벡터의 크기와 방향이 일정하게 유지된다고 할 수 있는 것입니다.

 

에너지-운동량 4차원 벡터에 들어가는 에너지는 정지질량 (rest-mass) 에너지와 운동에너지의 합이라고 할 수 있습니다. 질량-에너지 등가 원리에 따라서 질량을 가지고 있는 물체는 정지해 있는 상태에서도 에너지를 가집니다. 정지질량 에너지의 양은 질량에다가 광속의 제곱을 곱한 것, 즉 엠씨스퀘어로 주어지죠. 빛의 속도가 워낙 빠르기 때문에, 질량이 작아도 정지질량 에너지는 실로 어마무시합니다. 태양이 핵융합을 통해 지구에 쬐어주는 에너지와, 핵무기가 가진 가공할 만한 파괴력은 모두 정지질량 에너지로부터 나오는 것입니다.

 

한가지 더 짚고 넘어갈 점이 있다면, 물체의 운동량은 속력에 선형비례하지 않는다는 것입니다. 질량을 가진 물체의 속력이 광속에 접근함에 따라 그 에너지와 운동량이 무한대로 발산하게 되는데요. 이말인즉슨 물체를 가속시키기 위해 투입해야 하는 에너지의 양도 무한대가 됩니다. 그래서 특수상대론에 따르면 빛보다 빠르게 날아가는 광자로켓 같은 건 불가능합니다. 질량이 작은 소립자들은 적은 에너지로도 빠르게 가속시킬 수 있습니다만, 그럼에도 불구하고 빛의 속도를 뛰어넘은 사례는 지금까지 발견된 적이 없습니다.

 

특수상대론에서 물체의 에너지와 운동량이 어떻게 주어지는지를 이해하기 위한 한 가지 방법은 로렌츠 변환을 이용하는 것입니다. 시간과 공간이 결합된 민코프스키 시공간에서 여러 관찰자들이 측정한 물리량들의 상관관계를 알려주는 로렌츠 변환에 대한 더 자세한 내용은 다음 포스팅에 소개되어 있습니다.

 

물리학 상식 : 로렌츠 변환과 민코프스키 공간

 

각운동량

각운동량은 물체의 회전이나 공전으로 인해 발생하는 물리량입니다. 회전하는 물체가 얼마나 큰 임팩트를 줄 수 있는지를 수치화한 개념입니다.

 

각운동량을 이용해서 물리적인 피해를 주는 무기의 대표적인 예시로서 철퇴를 생각해볼 수 있죠. 손잡이가 달린 막대와 무게추가 사슬을 통해 연결되어 있는 형태의 철퇴들이 있습니다. 철퇴의 끝에 달린 무게추가 무겁고, 철퇴를 휘두르는 속도가 빠를수록 그 위력은 증가할 것입니다. 등속 원운동을 하는 무게추의 질량과 속력을 곱한 운동량이 증가함에 따라 철퇴의 위력이 증가한다고도 표현할 수 있겠습니다.

 

투사체를 발사하는 경우와는 달리 철퇴에는 공전 궤도 반지름이라는 또다른 변수가 있는데요. 막대기의 끝과 무게추를 연결한 사슬의 길이가 원운동의 반지름이 된다는 점을 생각해볼 수 있습니다. 철퇴를 휘두르는 속도가 동일하더라도 사슬의 길이에 따라 철퇴의 파괴력이 달라지죠. 즉 무게추의 공전 궤도 반지름이 길어질수록 그 위력이 증가하게 됩니다.

 

거리에 따라 임팩트가 어떻게 달라지는지에 대해 이해할 수 있는 또 다른 방법은 몸무게가 같은 두 사람이 시소를 타는 상황을 생각해보는 것입니다. 상대방을 들어올리기 위해서는 무조건 시소 끝에 가서 앉는 게 유리하죠. 반대로 시소의 중심에 가까워질수록 제가 올라갈 가능성이 높아지는 것입니다.

 

이러한 경험을 토대로, 원운동이 아닌 경우에 대해서도 적용할 수 있게 수학적으로 체계화한 개념이 바로 각운동량이라는 물리량입니다. 각운동량은 기준점으로부터의 위치 벡터와 운동량 벡터의 외적으로 주어집니다. 등속 원운동을 하는 물체의 각운동량은 궤도 반지름에다가 운동량의 크기를 곱한 것과 같고, 각운동량 벡터의 방향은 공전 궤도면에 수직이 됩니다.

 

 

벡터의 외적을 통한 정의로부터 유추할 수 있는 또 다른 특징은 기준점으로부터의 방향을 유지하는 방식으로 운동을 하는 물체라면, 각운동량이 0이 된다는 것입니다. 기준점에서 봤을때 이는 회전이나 공전운동이 없는 것이기 때문에 타당한 값이라고 볼 수 있죠.

 

운동량과는 달리 각운동량은 기준점을 어디로 잡느냐에 따라 그 크기와 방향이 달라진다는 특징도 있습니다. 그렇기 때문에 물리 문제를 풀 때 기준점의 위치를 일관적으로 유지해야 엉뚱한 결과를 맞이하지 않겠죠. 이는 여러개의 물체가 포함된 문제에 대해서도 마찬가지입니다.

 

다만 여러개의 물체로 이루어진 집합이 가진 각운동량을 계산할 때, 운동에너지의 경우와 비슷하게 문제를 단순화할 수 있습니다. 총 각운동량은 모든 물체를 무게 중심의 위치에 뭉뚱그렸을때의 점질량이 가지는 각운동량에다가 각 물체가 무게중심으로부터의 상대적인 운동에 따라 가지는 각운동량을 합친 것이라는 것입니다.

 

힘이 운동량을 발생시키는 점에 입각해서, 물체의 회전이나 공전을 유발하는 힘을 생각해볼 수 있습니다. 각운동량을 정의한 식을 시간에 대해서 미분하면, 각운동량의 시간 변화율을 얻을 수 있게 되고 각운동량을 발생시키는 돌림힘 (torque)이 어떻게 정의되는지 알 수 있는데요. 돌림힘은 기준점으로부터의 위치 벡터와 힘 벡터의 외적으로 주어집니다.

 

양자물리학과 관련된 글에서 단골로 등장하는 개념인 스핀 (spin angular momentum) 역시 그 정체는 각운동량입니다. 앞에서 설명한 궤도 각운동량과는 달리, 스핀은 입자 자체에 내재된 각운동량이라는 차이가 있습니다. 다시 말해서 스핀이 0이 아닌 입자의 경우, 회전이나 공전 운동을 하지 않을 때에도 각운동량을 가진다는 뜻이 됩니다.

 

---

 

물체에 작용하는 알짜힘 중에 운동 방향에 평행한 성분은 속력과 운동에너지를 바꾸지만, 운동 방향에 수직인 성분은 물체의 궤적을 휘어지게 만드는 효과가 있습니다. 이를 구심력이라고 하며 다음 포스팅에 더 자세한 내용이 소개되어 있습니다.

 

물리학 상식 : 원심력과 구심력

 

고등학교 지구과학 시간에 배우는 케플러 행성운동법칙 중의 2번째가 면적속도 일정의 법칙이죠. 태양과 행성 간의 가상의 직선을 상정하면, 이 직선이 단위 시간당 휩쓸고 지나가는 면적이 일정하다는 것이 그 핵심인데요. 이 법칙은 각운동량 보존이라는 물리적인 의미를 가지고 있습니다. 만유인력으로 인해 발생하는 돌림힘이 0이 된다는 것으로부터 유추할 수 있죠. 케플러 행성운동법칙에 대한 더 자세한 내용이 궁금하신 분들에게는 다음 포스팅을 읽어보시기를 권합니다.

 

물리학 상식 : 만유인력과 케플러 법칙

 

미시 세계에서 일어나는 일을 다루는 양자역학에서는 입자가 파동의 성질을 가지게 되고, 이는 물질파의 파동함수로 기술되는데요. 에너지와 운동량은 이 파동함수의 주파수와 파장과 관련이 있습니다. 이러한 파동-입자 이중성에 입각해서 위치와 운동량 간의 불확정성 원리 같은 중요한 결론들을 도출해낼 수 있죠. 여기에 대한 더 자세한 내용은 다음 포스팅에 소개되어 있습니다.

 

물리학 상식 : 파동-입자 이중성

 

이번 포스팅에서는 개별 입자나 물체가 가진 물리량들에 대해서 다루었지만, 수많은 분자들이 상호작용을 하면서 자유롭게 흐를 수 있는 유체 (fluid)의 운동을 수치화하기 위해서는 다른 방법을 쓰는 것이 좋습니다. 단위 부피나 단위 면적당 얼마나 많은 에너지와 운동량이 있는지를 따지는 것이 더 편리한데요. 이와 관련된 개념이 밀도와 압력이며, 다음 포스팅에 더 자세한 내용이 소개되어 있습니다.

 

물리학 상식 : 압력, 밀도와 상태 방정식

 

단단한 물체인 강체의 회전으로 인해 파생되는 각운동량과 운동 에너지를 다루기 위해서는 관성 모멘트 (moment of inertia)라는 개념을 도입하는것이 좋습니다. 관성 모멘트는 강체의 질량분포에 따라 결정되는 정사각행렬로서, 이를 통해 회전하는 강체의 각운동량과 에너지를 구하는 방법에 대한 더 자세한 내용은 다음 포스팅에 소개되어 있습니다.

 

물리학 상식 : 강체의 회전과 관성 모멘트

 

앞에서 언급한 스핀 각운동량을 다루기 위해서는 양자상태의 파동함수를 벡터로 다룰 필요가 있습니다. 스핀의 크기가 1/2인 입자의 경우 행과 열의 갯수가 2개인 정사각행렬을 통해서 스핀 각운동량을 나타낼 수 있고, 고유값 문제를 풀면 됩니다. 다음 포스팅에 예시로서 더 자세하게 소개되어 있습니다.

 

수학 상식 : 행렬의 고유값과 고유벡터