수학 상식 : 원통 좌표계와 구면 좌표계

벡터라는 개념을 처음 배울 때 사용했던 직각 혹은 데카르트 좌표계 (Cartesian coordinates) 이외에도, 풀고자 하는 수학이나 과학 문제에 따라 유용한 곡선 좌표계들이 있는데요. 3차원 공간에서는 원통 좌표계 (cylindrical coordinates)와 구면 좌표계 (spherical coordinates)가 대표적인 예시입니다. 여기서는 원통 좌표계와 구면 좌표계들이 어떻게 정의되고, 데카르트 좌표계와는 어떻게 연결되는지 살펴보겠습니다.

 

반응형

 

이름에서 유추할 수 있듯이 원통 및 구면 좌표계에서는 2차원 상의 원이나 3차원 상의 구면이라는 기하학적 개념을 상정하고 있습니다. 그렇기 때문에 삼각함수의 정의와 특징들을 먼저 알아둘 필요가 있는데요. 만약 삼각함수라는 개념이 생소하거나 이들에 대해 더 자세한 내용이 궁금하신 분들이라면, 시작하기에 앞서서 다음 포스팅을 읽어보는 것도 좋습니다.

 

수학 상식 : 원주율과 삼각함수

 

앞에서 언급했던 데카르트 좌표계에 대해서 간단히 말하자면, 서로 직각이 되는 축들을 상정하고 그 축 상의 위치를 통해 주어진 지점의 좌표를 표기하는 방식입니다. 예를 들어서 3차원 공간에서는 서로 직각인 x, y, z 축들이 있고, 주어진 점이 이들 축 위에 어떻게 대응되는지를 따져서 x, y, z 좌표를 구하게 됩니다.

 

원통 좌표계

원통 좌표계는 2차원 평면 상의 등방성 (isotropy)이 존재하는 상황에 최적화된 좌표계입니다. 주어진 지점을 x-y 평면 상에 투영했을때, 중심으로부터의 거리 (rho) 및 x축으로부터의 각도 (영어로 azimuthal angle, 그리스 문자 phi로 표기)를 통해 x 및 y 좌표를 특정할 수 있습니다. x-y 평면과 수직인 z축 방향은 데카르트 좌표계와 동일한 z 좌표를 그대로 활용합니다.

 

 

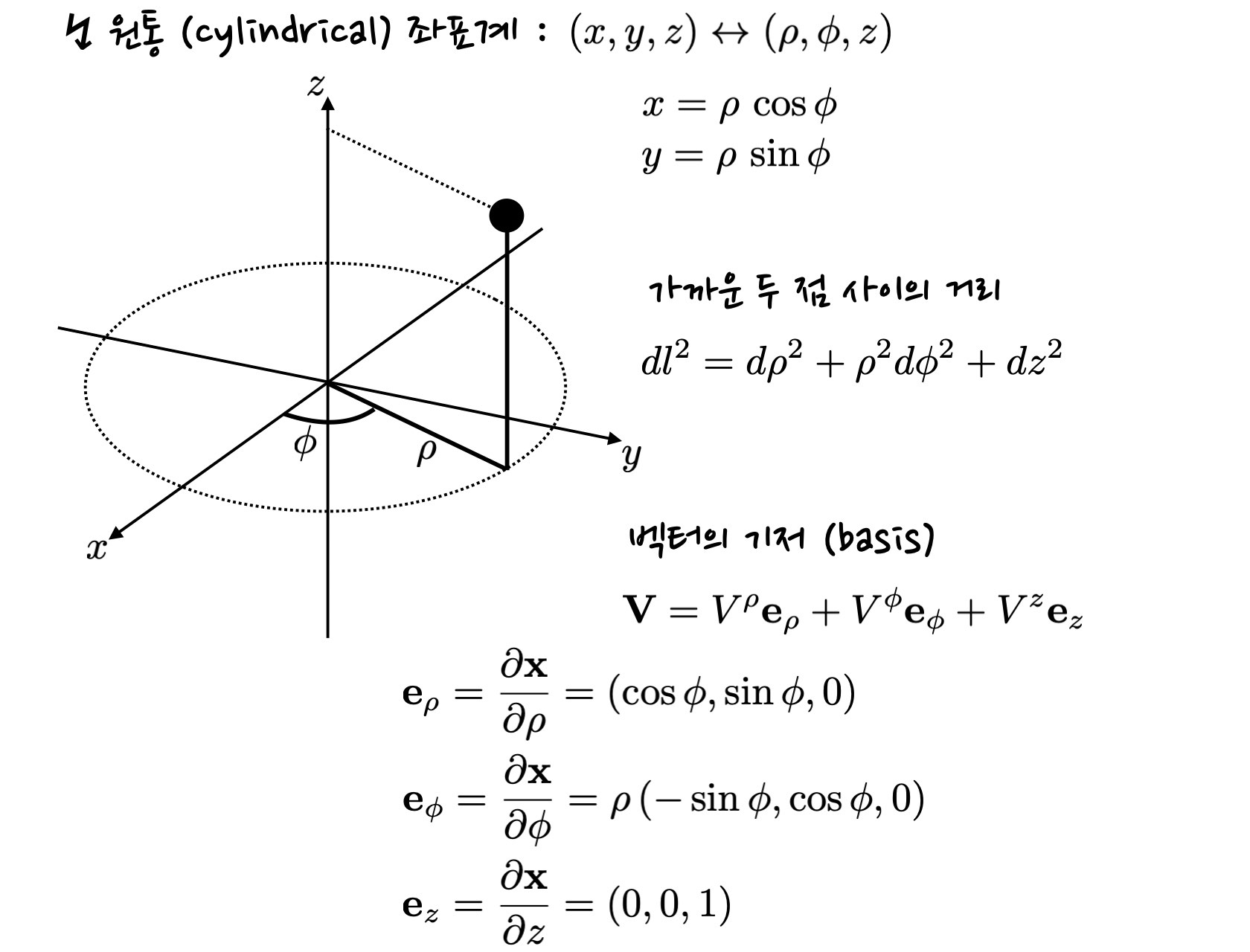
참고로 3차원 공간의 원통 좌표계에서 z 방향을 빼면, 2차원 공간의 극좌표계가 되는것도 특징입니다.

 

데카르트 좌표계의 경우와 비슷하게, 서로 직각을 이루는 3개의 기저 (basis) 벡터들이 존재하고, 임의의 벡터를 기저 벡터들의 선형 결합으로 나타내는 것이 가능합니다. 한 가지 주의할 점이 있다면, 이 기저 벡터들의 방향이 위치에 따라 달라진다는 것인데요. 벡터를 미분하는데 있어서 각 방향의 성분 뿐만 아니라, 기저 벡터의 방향이 변하는것 까지 고려해야 하는 것입니다.

 

원통 좌표계를 활용해 볼 만한 예시 중의 하나로 원형 드럼의 표면을 생각해 볼 수 있는데요. 드럼을 치면서 표면이 어떻게 떨리는지를 묘사하고자 할 때, 각 지점에서의 표면의 높이를 z축으로 상정할 수 있습니다. 비슷하게 원형 모양의 대야에 받아놓은 물에서 물결파가 어떻게 발생하는지를 알아보는데에도 원통 좌표계가 유용합니다.

 

벡터 장 (vector field)을 대상으로 하는 몇 가지 미분 연산자들이 어떻게 정의되는지에 대해서도 알아두면 좋습니다. 대표적으로 발산 (divergence), 라플라스 (Laplacian) 연산자, 회전 (Curl)이 있죠. 앞서 언급했듯이 위치에 따라 기저 벡터들의 방향이 달라지기 때문에, 데카르트 좌표계의 경우에 비해 더 복잡한 형태를 띠고 있습니다.

 

 

구면 좌표계

구면 좌표계는 3차원 공간에서 등방성이 존재하는 상황에 안성맞춤인 좌표계입니다. 주어진 지점을 x-y 평면에 투영했을 때 x축으로부터의 각도 (phi)가 사용되는 점은 원통 좌표계와 동일합니다. 반면에 구면 좌표계에서는 중심으로부터 3차원 공간 내의 거리 r 및 z축으로부터의 각도 (영어로 polar angle, 그리스 문자 theta로 표기)가 들어갑니다.

 

 

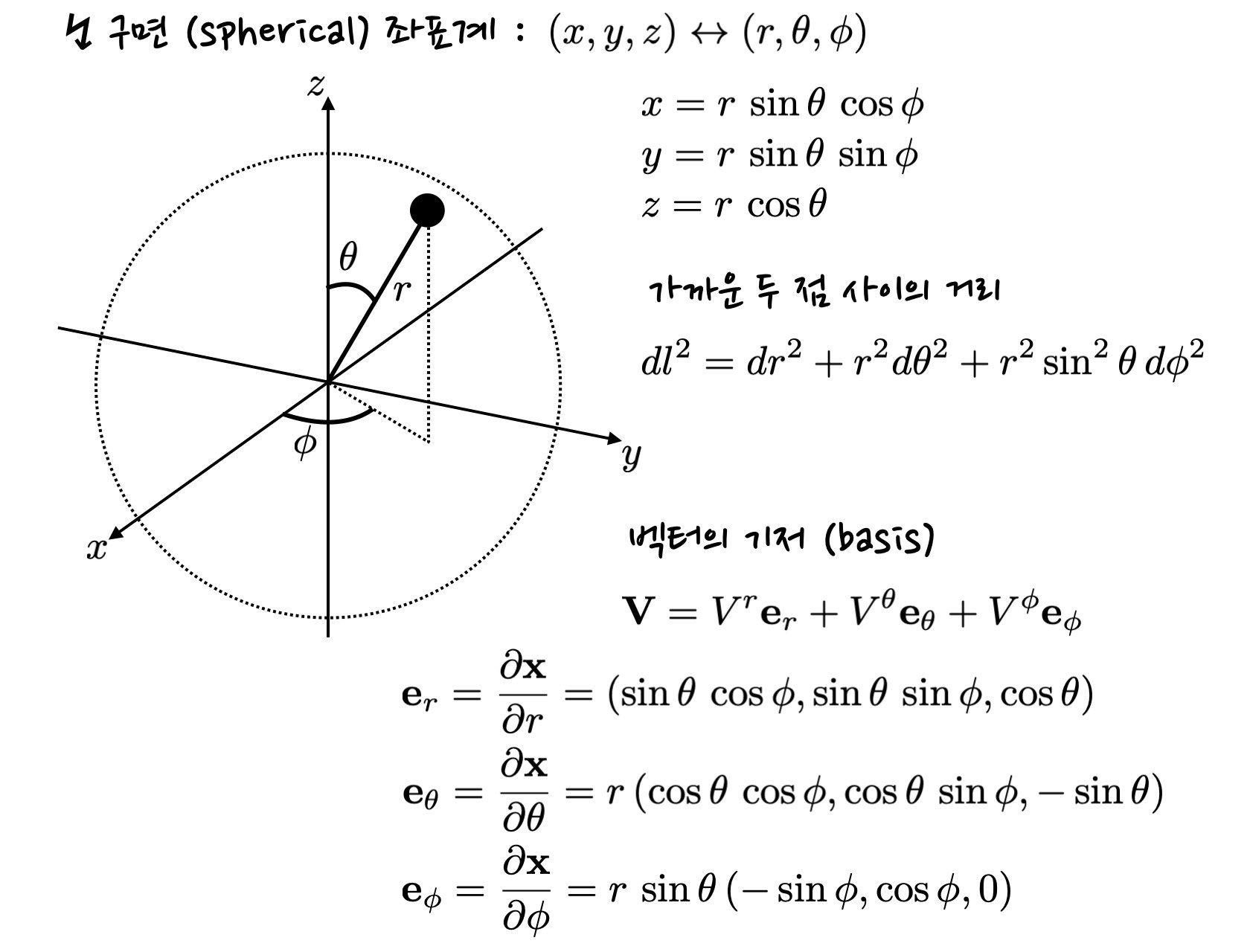
구면 좌표계에서 중심으로부터의 거리를 일정하게 유지하면, 2차원 구면 상의 위치를 나타내는 좌표계로 활용할 수 있습니다. 지구상의 위도와 경도와 비슷한 개념이죠. 구면 좌표계에서는 북극으로부터의 각도가 있고, 위도는 적도를 그 기준으로 한다는 차이점이 있습니다만, 기본 취지는 동일합니다.

 

원통 좌표계에서와 비슷한 방식으로 3개의 기저 벡터들을 정의할 수 있고, 이들은 서로 직각을 이룬다는 것도 확인이 가능합니다. 뿐만 아니라 위치에 따라 방향이 변하는 것도 주목할 필요가 있겠습니다.

 

구면 좌표계를 활용할 수 있는 대표적인 예시로서 점질량에 의한 중력장이 있습니다. 태양 주위를 공전하는 행성의 케플러 운동을 계산하는 경우를 생각해볼 수 있는데요. 물론 태양 자체는 유한한 크기를 가지고 있습니다만, 행성 궤도의 크기에 비하면 매우 작을 뿐더러 태양의 형태도 구에 가깝기 때문에, 태양으로 인한 중력장 역시 모든 방향에서 동일한 등방성을 가지고 있죠. 비슷한 논리로 수소 원자에 소속된 전자의 파동함수를 구하는 데 있어서도 구면 좌표계가 사용됩니다.

 

원통 좌표계와 마찬가지로 벡터 장에 대한 미분 연산자들을 정의할 수 있습니다.

 

 

앞서 언급했듯이 태양의 중력에 따른 행성의 공전을 설명하는 데 구면 좌표계를 활용할 수 있습니다. 뉴턴 운동 방정식의 해를 구하고 이로부터 케플러 법칙들을 도출하는 과정은 다음 포스팅에 더 자세하게 소개되어 있습니다.

 

물리학 상식 : 만유인력과 케플러 법칙

 

---

 

같이 알고 있으면 좋은 수학 지식

 

위도와 경도

수학 상식 : 위도, 경도와 도법

 

미분과 적분

수학 상식 : 미분과 적분 이해하기

 

테일러 급수 전개

수학 상식 : 테일러 급수 전개