수학 상식 : 원주율과 삼각함수

여기서는 기하학에 관련된 중요한 상수인 원주율과, 과학 및 공학 분야에서 가장 흔하게 접할 수 있는 주기함수인 삼각함수에 대해 얘기해볼까 합니다.

 

반응형

 

원주율과 호도법

먼저 유클리드 공간에서 원주율을 정의하는 방법과, 각도를 나타내는 방법인 호도법에 대해 알아봅시다. 유클리드 공간이란 간단히 말하자면 두 점 사이의 직선거리를 피타고라스 정리로 구할 수 있는 평탄한 공간을 이야기합니다. 피타고라스 정리가 통하지 않는 비유클리드 공간의 대표적인 예시로 구면이 있죠. 유클리드 공간에서 원을 그렸을 때, 원의 둘레와 지름 사이의 비율은 원의 크기와 무관하게 일정한 값을 가지는데요. 원의 둘레를 지름으로 나눈 일정한 비율의 값이 바로 원주율입니다. 보통 그리스 문자 파이 (pi)로 표시하며, 그 값을 소수점 10번째 숫까까지 쓰면 3.1415926536 이 되겠습니다.

 

그 다음으로 호도법에 따라 각도를 나타내는 단위인 라디안 (radian)에 대해 간략히 살펴봅시다. 먼저 부채꼴의 호의 길이는 중심각의 크기에 비례한다는 점에 주목할 필요가 있습니다. 즉 반지름이 1인 부채꼴이 있을 때, 호의 길이와 중심각의 크기 사이에는 1대1 대응이 성립하죠. 이러한 호의 길이를 가지고 각도를 표시하는 것이 바로 호도법입니다.

 

 

흔히 일상생활에서는 각도를 도 (degree)단위로 표시하는데, 이것 역시 라디안 단위와 1대1 대응 관계를 가지고 있습니다. 예를 들어서 반지름이 1인 원을 한바퀴 돌아서 원래 위치로 돌아왔다면, 이는 360도에 해당하죠. 원의 지름이 2인 관계로, 호도법에 따라 라디안 단위로 나타내면 이는 원주율의 2배입니다. 비슷하게 180도를 라디안 단위로 변환하면 그 크기는 원주율의 값과 동일하고요. 또한 90도를 라디안 단위로 쓰면 원주율의 절반이 되겠습니다.

 

호도법에 익숙해지면 실용적인 측면에서도 좋습니다. 대표적인 예시로는 C언어 또는 C++ 를 이용한 프로그래밍이 있는데요. 수학 함수 라이브러리에 정의되어 있는 삼각함수 및 역삼각함수들이 라디안 단위를 상정하고 있기 때문입니다. 예를 들어서 180도를 삼각함수의 인자로 주고 싶을때는 호도법에 따라 원주율의 값을 입력해야 합니다. 만약 180이라는 숫자를 줘 버린다면, 완전히 엉뚱한 결과를 맞이하게 되겠죠.

 

제목에도 나와 있는 삼각함수를 미리 언급 해 버렸는데, 그게 뭔지 더 자세히 살펴봅시다.

 

삼각함수

주기함수 중에서 수학적으로 가장 우아하다고 여겨지는 것이 삼각함수입니다. 우아하다는 수식어가 걸맞는 이유 중 하나는 2차원 평면 상의 원으로부터 그 정의를 쉽게 도출해낼 수 있다는 점을 들고 싶습니다. 참고로 주기함수는 일정한 패턴이 반복되는 함수를 말하는데요. 수학적으로 좀 더 엄밀히 정의하자면, 함수의 인자에 주기만큼의 값을 더했을 때 기존 인자의 함수 값과 동일해지는 것이 주기함수입니다. 본론으로 돌아가서 삼각함수의 정의에 대해 알아봅시다.

 

 

2차원 평면 상에 반지름이 1이고 중심이 원점에 있는 원이 하나 있습니다. 가로축 x 와 세로축 y 의 값이 각각 1, 0인 지점에서 시작해서, 반시계 방향으로 원을 따라 돌아가는 상황을 상정해 봅시다. 그러면 초기 위치로부터 중심각의 값에 따라 현재 위치의 x 와 y 좌표 값들이 바뀌겠죠. 이 좌표들의 값이 바로 삼각함수의 값이라고 볼 수 있습니다. 즉 x 좌표의 값은 중심각을 매개변수로 하는 코사인 (cosine, 줄여서 cos)함수, y 좌표의 값은 사인 (sine, 줄여서 sin)함수가 되는 것입니다. 원을 따라서 한바퀴 돌면 본래 위치로 돌아오기 때문에, 삼각함수의 주기는 360도 혹은 2pi 라디안이 됩니다.

 

삼각함수들의 또 다른 특징으로는 코사인 함수의 제곱과 사인 함수의 제곱을 더하면 항상 1이 된다는 것입니다. 이는 인자로 들어가는 각도와 무관하게 성립하며, 기하학적으로 보면 삼각함수의 정의를 위해 언급한 원의 반지름이 1인 것과 관련이 있죠.

 

자매품으로는 탄젠트 (tangent, 줄여서 tan)함수가 있는데요. 이는 사인함수를 코사인 함수로 나눈 함수입니다. 한 가지 짚고 넘어갈 점이라면, 탄젠트 함수의 값이 무한대로 발산할 수 있다는 것입니다. 분모에 들어가는 코사인 함수가 각도에 따라 0이 될 수 있기 때문이죠.

 

삼각함수들의 미분은 다음과 같이 계산할 수 있습니다.

 

 

인자로 들어가는 각들의 합에 따라 삼각함수가 어떻게 나타나는지에 대한 덧셈정리도 알아두면 유용합니다. 고등학교 수학시간에 배우는 내용이죠.

 

 

이 덧셈정리를 증명하는 방법은 2차원 상에서의 회전변환 등 여러가지가 있습니다만, 오일러 공식을 이용해서 증명할 수도 있습니다. 이를 위해서는 삼각함수를 지수함수와 연계해서 이해할 필요가 있는데요. 지수함수와 오일러 공식에 대한 자세한 사항은 다음 포스팅에 소개되어 있습니다.

 

수학 상식 : 지수함수와 로그함수

 

벡터의 곱셈 연산인 내적과 외적이 가지는 기하학적인 의미를 이해하기 위해서도 삼각함수에 대해 알아둘 필요가 있습니다. 벡터의 덧셈과 곱셈에 대해 더 자세한 내용이 궁금하시다면, 다음 포스팅을 읽어보는 것을 권합니다.

 

수학 상식 : 벡터의 덧셈과 곱셈 (내적, 외적)

 

아울러 삼각함수들을 통해 원통 좌표계나 구면 좌표계를 상정하면, 등방성이 존재하는 수학 및 과학 문제들을 좀 더 손쉽게 풀 수 있습니다. 더 자세한 내용은 다음 포스팅에 소개되어 있습니다.

 

수학 상식 : 원통 좌표계와 구면 좌표계

 

구면에 가까운 지구 표면 상의 지리 정보를 평면 상에 투영하여 지도를 만드는 데에도 삼각함수가 사용됩니다. 더 자세한 내용이 궁금하신 분들에게는 다음 포스팅이 큰 도움이 되리라 생각합니다.

 

수학 상식 : 위도, 경도와 지도 투영법

 

역삼각함수

역삼각함수는 말 그대로 삼각함수의 역함수입니다. 즉 삼각함수들의 값을 인자로 받은 다음 각도를 돌려주는 함수죠. 삼각함수들이 가질 수 있는 값의 범위가 정의역으로 주어지고, 주기의 절반이 공역으로 주어진다는 특징이 있습니다. 코사인, 사인, 탄젠트 함수의 역함수들을 각각 아크코사인 (arccos 또는 acos), 아크사인 (arcsin 또는 asin), 아크탄젠트 (arctan 또는 atan)라고 부릅니다.

 

 

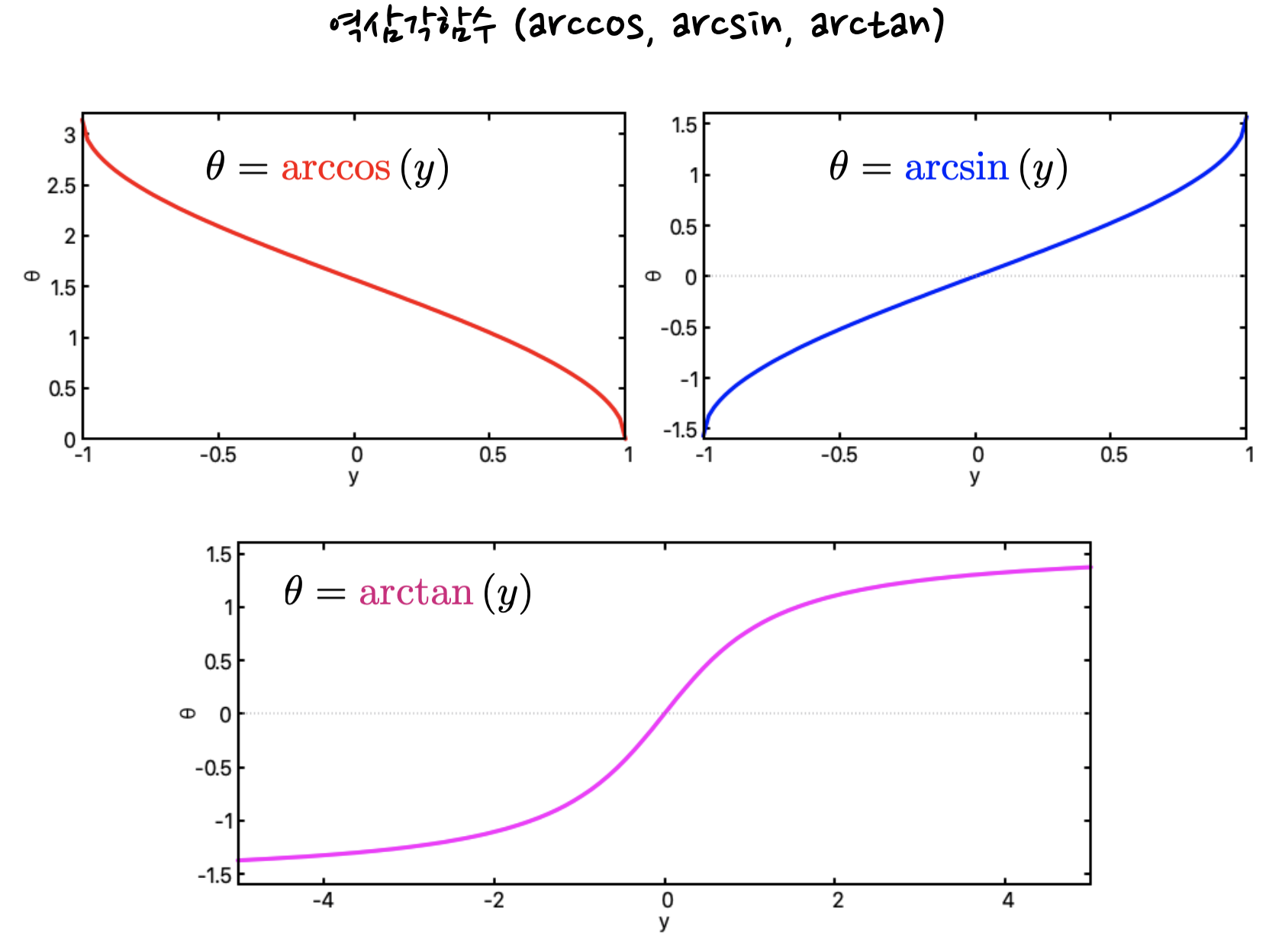
역삼각함수를 이용해서 원주율의 값을 직접 계산해볼 수도 있는데요. 가장 쉬운 방법으로는 아크탄젠트를 미분하여 얻은 도함수를 특정 구간에 대해 적분하는 것입니다. 라디안 단위로 원주율의 4분의 1에서는 탄젠트 함수가 1이 되고, 원주율의 절반에서 탄젠트 함수가 무한대로 발산한다는 것을 이용한 방법이죠.

 

 

이 적분을 직접 계산해도 되고, 테일러 전개를 통해 이를 무한급수로 변형한 다음 원주율의 값을 구하는 것도 가능합니다. 하지만 어떤 방식을 취하더라도 펜과 종이만 가지고는 이를 계산하기가 쉽지 않습니다. 그렇기 때문에 컴퓨터의 도움을 받는것이 좋겠죠. C언어를 이용해서 이를 수치적으로 계산하는 방법이 궁금하시다면, 다음 포스팅을 읽어보시기를 권합니다.

 

C/C++ 원주율 계산 프로그램

 

이상으로 원주율과 삼각함수가 어떻게 정의되고 어떻게 생겼는지에 대해 알아보았습니다. 삼각함수는 파동 현상을 이해하는 데 있어서 필수적인 수학적 도구인데요. 파동에 대한 자세한 내용은 다음 포스팅을 참고하면 좋습니다.

 

물리학 상식 : 파동의 이해

 

---

 

같이 알고 있으면 좋은 수학 지식

 

테일러 급수 전개

수학 상식 : 테일러 급수 전개