수학 상식 : 위도, 경도로부터 최단거리 계산하기

이번 포스팅에서는 지구 상의 위도와 경도를 알고 있는 두 도시간의 최단거리를 계산하는 방법에 대해 알아봅시다. 최단 경로에서 위도와 경도가 어떻게 달라지는지를 알아내기 위해서는 복잡한 계산을 해야 하지만, 최단경로의 길이는 삼각함수가 포함된 비교적 단순한 계산을 통해 알 수 있습니다.

 

반응형

 

앞에서 삼각함수를 언급했는데, 코사인 (cosine) 함수 및 사인 (sine) 함수들의 특징에 대해 알아둘 필요가 있습니다. 삼각함수의 정의와 특징에 대해서는 다음 포스팅에 더 자세한 내용이 소개되어 있습니다.

 

수학 상식 : 원주율과 삼각함수

 

두 도시간의 최단거리를 구하기 위해서 벡터의 내적 또는 스칼라 곱을 사용하게 될텐데요. 내적의 정의와 기하학적인 의미에 대한 더 자세한 내용이 궁금하시다면, 다음 포스팅이 큰 도움이 되리라 생각합니다.

 

수학 상식 : 벡터의 덧셈과 곱셈 (내적, 외적)

 

덧붙여 최단거리를 구하고자 하는 두 도시의 위치를 알아야 하는데, 이는 위도와 경도라는 구면 상의 좌표를 통해서 알 수 있습니다. 위도 및 경도의 정의와, 이를 이용해 지구 표면상의 위치를 특정하는 방법에 대해서는 다음 포스팅에 더 자세하게 소개되어 있습니다.

 

수학 상식 : 위도, 경도와 지도 투영법

 

수학적 원리

첫 번째 단계로서, 지구 중심으로부터 표면 상의 특정 지점으로 향하는 3차원 위치 벡터를 상정해볼 수 있습니다. 이 벡터의 크기는 지구의 반지름과 동일하겠죠. 그리고 지구의 자전축을 z축 방향으로 잡았을 때, 벡터의 x, y, z축 방향의 성분을 위도와 경도를 이용해서 정의할 수 있을 것입니다. 이 때 삼각함수가 동원됩니다.

 

 

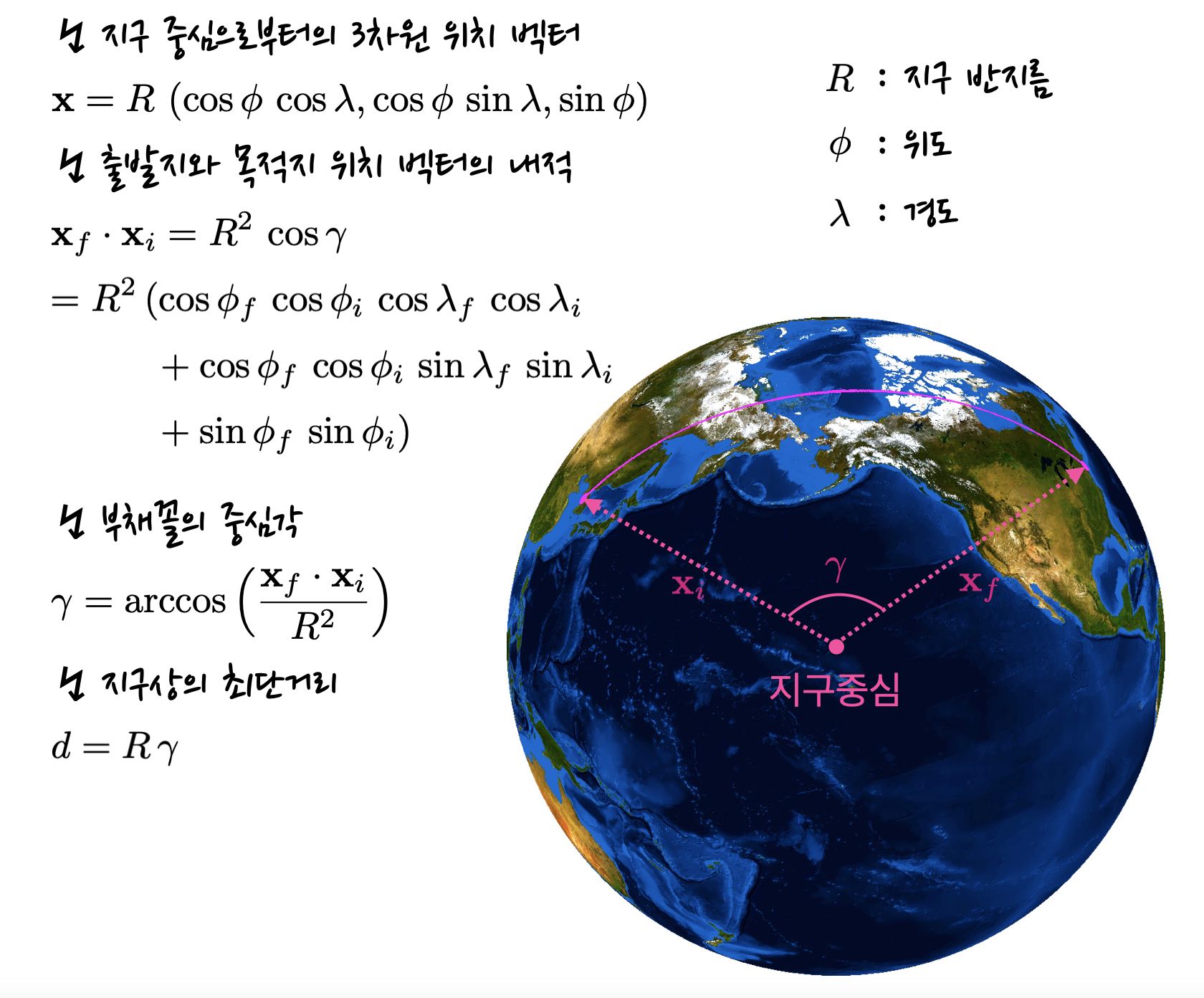
그러면 최단거리를 구하고자 하는 두 도시의 위치 벡터들의 내적을 구할 수 있게 됩니다. 그리고 내적은 두 벡터가 이루는 각도의 코사인 값에 비례한다는 기하학적인 의미를 가지고 있죠. 이러한 점에 입각해서, 지구 중심과 출발지 및 목적지가 이루는 부채꼴의 중심각을 구할 수 있게 되겠습니다.

 

마지막 단계는 부채꼴의 중심각을 호도법으로 나타낸 뒤, 여기에 지구 반지름을 곱해서 최단거리를 구하는 것입니다. 이 최단거리를 항공기의 순항속도로 나누게 되면, 대략적인 비행시간도 구할 수 있습니다.

 

C/C++ 프로그램

앞에서 언급한 수학적인 정의를 바탕으로 간단한 프로그램을 만들어볼 수 있습니다. 출발지와 목적지의 위도와 경도를 입력받은 뒤에, 최단거리를 계산해서 출력하는 프로그램입니다. 이번 포스팅에서는 C언어 프로그램을 소개합니다만, 다른 프로그래밍 언어로도 동일한 수학적 원리를 적용해서 프로그램을 만드는 것이 가능합니다.

 

소스 코드입니다.

 

#include<math.h>

// 지구 반지름 (km 단위)
double radius_earth = 6378.;

/* 도 (degree)와 라디안 단위
 * 사이의 비례상수 */
double fac_deg_to_rad = M_PI / 180.;

/* 출발지와 목적지의 위도와 경도를 매개변수로 받아서
 * 최단거리를 계산하는 함수
 * lat_origin : 출발지의 위도
 * lat_target : 도착지의 위도
 * lng_origin : 출발지의 경도
 * lng_target : 도착지의 경도
 * 각도는 라디안 단위 */
double get_dist_on_earth(double lat_origin,
                         double lat_target,
                         double lng_origin,
                         double lng_target) {
    double cos_gamma =
        cos(lat_target) * cos(lat_origin) *
        cos(lng_target) * cos(lng_origin) +
        cos(lat_target) * cos(lat_origin) *
        sin(lng_target) * sin(lng_origin) +
        sin(lat_target) * sin(lat_origin);

    double gamma = acos(cos_gamma);

    return radius_earth * gamma;
}

// main 함수
int main(int argc, char *argv[]) {
    double lat_i, lat_f;
    double lng_i, lng_f;

    // 출발지의 위도, 경도 입력
    fprintf(stdout, "latitude of origin (degree) : ");
    scanf("%lf", &lat_i);
    lat_i *= fac_deg_to_rad;
    fprintf(stdout, "longitude of origin (degree) : ");
    scanf("%lf", &lng_i);
    lng_i *= fac_deg_to_rad;

    // 도착지의 위도, 경도 입력
    fprintf(stdout, "latitude of target (degree) : ");
    scanf("%lf", &lat_f);
    lat_f *= fac_deg_to_rad;
    fprintf(stdout, "longitude of target (degree) : ");
    scanf("%lf", &lng_f);
    lng_f *= fac_deg_to_rad;

    // 최단거리 계산
    double distance =
        get_dist_on_earth(lat_i, lat_f, lng_i, lng_f);

    // 최단거리를 km 단위로 출력
    fprintf(stdout, "\n");
    fprintf(stdout,
        "The shortest distance (km) : %e\n", distance);

    return 0;
}

 

최단거리를 가지는 경로를 따라 갈 때 위도와 경도가 어떻게 변하는지 파악하기 위해서는 좀 더 복잡한 미분방정식을 풀어야 합니다. 이러한 방정식을 지름길 방정식 (geodesic equation)이라고 하는데요. 지름길 방정식을 수치적으로 풀어서 항공기의 대략적인 비행경로를 구하는 법에 대해서는 다음 포스팅에 더 자세히 소개되어 있습니다.

 

C/C++ 반복-이완 계산법으로 알아보는 비행경로