C/C++ Runge-Kutta 방법으로 알아보는 인구역학

목차

1. 로지스틱 방정식
   
   
2. 확장된 가설 : 어른과 어린이
   
   
3. 확장된 가설 : 인간과 삼림

 

인터넷을 돌아다니다가 우연히 인구역학 (population dynamics) 및 이를 위한 수학적 모형에 대한 설명을 위키 페이지에서 읽게 되었습니다. 본래 검색 의도에 맞는 결과는 아니었지만, 수학 모형에 혹해서 결국 관심있게 읽게 되었네요.

 

Population dynamics - Wikipedia

 

인구역학이라는 것은, 간단히 말해서 다양한 생물종의 연령대별 개체 수가 시간에 따라 어떻게 진화하는지를 수학적으로 규명하기 위한 생물학의 한 갈래라고 합니다. 수치해석을 통해서 인구역학에 대해 간략히 알아볼까 합니다.

 

반응형

 

로지스틱 방정식

가장 단순한 수학적 모형으로는 로지스틱 (logistic) 방정식이 있는데요. 개인적으로 이 주제에 흥미를 가지게 된 이유가, 방사성 붕괴로 인한 동위원소 개수의 변화를 기술하는 방정식과 그 형태가 유사하기 때문이었습니다. 인구역학에서 등장하는 로지스틱 방정식의 주요 상수로는 자연적인 개채수 증가율 (growth rate) 및 주어진 환경에서 부양 가능한 최대 개체 수 (carrying capacity)가 있다는군요.

 

로지스틱 방정식 - 위키백과, 우리 모두의 백과사전

 

 

자연적인 개체수 증가율 및 부양 가능한 최대 개체 수가 시간에 따라 변하지 않는 진짜 상수인 경우에 한해, 수치해석을 하지 않고도 로지스틱 방정식의 해석적인 해를 구할 수 있습니다. 그래도 C++ 수치해석을 통해서 해를 구하고 해석적인 결과와 비교를 해볼텐데, 이는 제가 만든 수치해석 프로그램의 유효성을 검증하기 위한 방법 중 하나이기 때문입니다. 답을 모르는 미지의 영역에서 컴퓨터가 내놓은 답을 신뢰하기 위해서는, 먼저 제가 잘 아는 문제에 대한 답을 재현할 수 있다는 걸 확인할 필요가 있는것이죠.

로지스틱 방정식을 수치적으로 다루기 위해 다음과 같은 C++ 프로그램을 사용했습니다.

ODESolveRK.h [다운로드]

ODESolveRK.cpp [다운로드]

위의 헤더 파일 및 소스파일에 도입되어 있는 ODESolveRK 클래스는 진자운동에 대한 예전 포스팅에 나온 것과 동일한 코드를 사용했습니다.

 

C/C++ Runge-Kutta 방법으로 알아보는 진자운동

 

또 다른 소스파일에서는 main 함수와 더불어 풀고자 하는 상미분 방정식의 형태와 초기조건을 정하게 됩니다.

test1_population_RK4.cpp [다운로드]

 

#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<math.h>
#include<vector>
#include"ODESolveRK.h"

/* time is multiplied by the natural growth rate Gamma,
 * while population is divided by the carrying capacity K.
 * By doing that,
 * we can deal with dimensionless quantities. */

const double t_ini = 0.;  // initial time
const double t_fin = 5.;  // final time
const double delta_t = 0.02;  // size of timestep in RK
const double n_ini = 0.4;  // initial population (N at t_ini)

// time derivative of population
double dn_dt(double t, double *n);
/* analytic solution
 * to the logistic equation */
double func_sol_logistic(double t);

int main(int argc, char *argv[]) {
    /* array of function pointer for time derivatives
     * of population */
    func_oderk_deriv *ptr_in_func;
    ptr_in_func =
        (func_oderk_deriv *)malloc(sizeof(func_oderk_deriv) * 1);
    ptr_in_func[0] = &dn_dt;

    /* arrays to store the evolution history
     * of population */
    int nbin_t = (int)floor(fabs(t_fin - t_ini) / delta_t + 1e-8);
    double *t_history;
    std::vector<double> *n_history;
    t_history = new double [nbin_t + 1];
    n_history = new std::vector<double> [nbin_t + 1];

    t_history[0] = t_ini;
    n_history[0].clear();
    n_history[0].push_back(n_ini);

    ODESolveRK ode_solver;
    // initialize the ODE Runge-Kutta solver
    bool initialized =
        ode_solver.init(1, t_history[0], n_history[0], ptr_in_func);

    for (int it = 1; it <= nbin_t; it++) {
        bool go_next = ode_solver.next_RK4(delta_t);
        if (!go_next) {
            break;
        }

        ode_solver.get_system_current(t_history[it], n_history[it]);
        fprintf(stderr, "  %e  %e  %e\n", t_history[it],
            n_history[it].at(0), func_sol_logistic(t_history[it]));
    }

    char filename_prefix[200];
    char filename_extend[200];

    bool fname_arg_prefix = argc >= 2;
    if (fname_arg_prefix) {
        strcpy(filename_prefix, argv[2]);
    } else {
        strcpy(filename_prefix, "population_logistic");
    }

    bool fname_arg_extend = argc >= 3;
    if (fname_arg_extend) {
        strcpy(filename_extend, argv[2]);
    } else {
        strcpy(filename_extend, "dat");
    }

    char buffer[10];
    sprintf(buffer, "%f", n_ini);

    FILE *fout;
    char filename_out[200];
    strcpy(filename_out, filename_prefix);
    strcat(filename_out, "_n0_");
    strcat(filename_out, buffer);
    strcat(filename_out, ".");
    strcat(filename_out, filename_extend);
    fout = fopen(filename_out, "w");
    fprintf(fout, "# n0/K = %e\n", n_ini);
    fprintf(fout, "# [Gamma t]  [N/K numerical]  [N/K analytic]\n");

    for (int it = 0; it <= nbin_t; it++) {
        fprintf(fout, "  %e  %e  %e\n", t_history[it],
            n_history[it].at(0), func_sol_logistic(t_history[it]));
    }

    fclose(fout);

    delete [] t_history;
    delete [] n_history;
    free(ptr_in_func);

    return 0;
}

double dn_dt(double t, double *n) {
    return n[0] * (1. - n[0]);
}

double func_sol_logistic(double t) {
    return n_ini / (n_ini + (1. - n_ini) * exp(t_ini - t));
}

 

GNU C++ 컴파일러를 이용할 경우 다음과 같이 컴파일 및 링크하여 실행파일을 얻을 수 있습니다.
  g++ ODESolveRK.cpp -c
  g++ test1_population_RK4.cpp -c
  g++ test1_population_RK4.o ODESolveRK.o -lm -o [실행파일 이름]

프로그램을 돌려 보면, 아래 그래프와 같이 수치해석으로 얻은 결과를 나타낸 사각형 점들이 해석적인 해를 나타내는 곡선들과 잘 일치한다는 걸 볼 수 있습니다.

 

 

현재 개체 수가 부양 가능한 최대치보다 낮을 때는 개체 수가 증가합니다. 반면에 주어진 환경이 부양할 수 있는 능력에 비해 개체 수가 많으면, 감소하게 되는 걸 볼 수 있죠. 결과적으로 개체 수는 부양 가능한 최대치로 수렴하게 됩니다. 개체 수는 실제로 자연수이지만, 모형에서는 유리수 및 무리수를 포함하는 실수로 간주되는데요. 이는 서로 같은 초기조건 및 환경을 가지고 있으면서도, 완벽히 분리된 생태계들에게서 얻어진 평균값 정도로 생각하면 무리가 없을 것 같습니다.

이 로지스틱 방정식 및 함수는 여러 생물군의 개체 수를 모델링하는데 있어서 성공적이었다고 합니다만, 여전히 비현실적인 구석들이 있습니다. 예를 들어서, 실제로는 개체 수 증가가 특정 시기에 발생하지만 로지스틱 방정식은 시간에 따른 연속적인 증가를 가정하고 있습니다. 또한 어른과 아이의 숫자가 동일한 방식으로 증가 및 감소한다는 것 역시 비현실적인 부분이라 할 수 있겠네요.

 

목차로 ...

 

확장된 가설 : 어른과 어린이

기존의 로지스틱 방정식을 확장하여, 성인 (adult) 및 어린이 (child)의 인구수를 분리해서 새로운 가설을 세워 보았습니다. 미리 강조할 점이 하나 있다면, 저는 생물학 전공자가 아닌 관계로 이것 역시 개인적인 호기심으로 인해 만들어진 단순한 모형이라는 것인데요. 불완전하거나 틀린 내용이 있을 수 있으므로, 관련 전공자분들이 저를 깨우쳐주기 위한 목적으로 하는 태클이라면 언제든지 환영입니다.

 

 

총 인구 수를 성인 인구 N_adult 와 영유아 인구 N_child 로 분리했고, 이들은 시간에 대한 함수로서 미분방정식에 의해 그 형태가 결정됩니다. 더 현실적인 모형을 만들기 위해, 로지스틱 방정식보다 더 많은 변수를 고려하고 있는데요.

 

• 신체 성장률 Gamma_growth
  어린이 1명이 성인이 되기까지 얼마나 걸리는지에 관련된 수치입니다. 만 0세부터 14세까지를 영유아라고 하고, 그 이상의 나이를 성인의 기준으로 잡게 되면, 출생부터 성인이 되기까지 15년이 걸리므로 신체 성장률은 1 분의 15년이라고 보면 되는거죠.
• (유효) 출산율 Gamma_birth
  성인 1명이 단위시간동안 평균적으로 몇 명의 아이를 낳는지와 관련된 수치입니다. 영유아 인구의 시간 변화율을 나타내는 방정식의 맨 첫번째 항이 출산율과 관련된 것인데요. 성인의 수가 증가함에 따라 감소하는 지수함수의 존재로 인해 Gamma_birth 자체는 출산율과 다릅니다. 그럼에도 불구하고 Gamma_birth 의 값이 증가할수록 영유아 인구의 증가율이 높아지므로 유효 (effective) 출산율이라는 이름을 대신 붙였습니다.
• 성인 사망률 Gamma_death,ad
  단위시간동안 성인 전체 인구 대비 사망자 수의 비율을 나타냅니다. 평균수명을 60세로 가정하고, 만 15세부터 성인이라고 간주하면 평균적으로 45년 가량을 성인으로 살게 되겠죠. 그러면 사망률은 1분의 45년 정도로 잡으면 되겠습니다.
• 영유아 사망률 Gamma_death,ch
  성인 사망률과 비슷한 개념이지만, 영유아의 사망자 수를 수치화 한 것입니다. 성인 사망률과는 달리 외부적 요인이 많이 반영될텐데요. 예를 들어서 사회가 안정적이고 보건 인프라가 잘 갖춰진 선진국이라면, 영유아 사망률이 거의 없다고 봐도 무방합니다. 반면에 후진국이나 고대사회의 경우 영유아 사망률이 높은 것과 동시에, 높은 출산율로 이를 커버한다는 특징이 있습니다.
• 인구 부양력 K'
  로지스틱 방정식에 등장하는 부양 가능한 최대 개체 수와 비슷한 포지션을 가지고 있습니다. 이 수치는 출산율과 관련된 항의 지수함수 안에서 등장하는데요. 이 지수함수의 형태는 로지스틱 방정식에서 인구증가가 억제되는 방식으로부터 착안한 것입니다. 인구 부양력이 상수인 경우, 인구가 일정하게 유지되는 평형 상태의 인구 수는 부양력 K' 에 비례한다는 특징도 가지고 있습니다.

 

이 모형을 기반으로, 특정 시점에 인구 부양력이 2배로 증가한 시나리오를 상정해서 시뮬레이션을 해 보았습니다. 예컨대 산업화가 진행되면서 재화의 생산이 늘어난다면, 미래 세대에 대한 낙관적인 전망이 자리잡고 출산율이 오르겠죠.

 

test2_population_RK.ccp [다운로드]

 

#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<math.h>
#include<vector>
#include"ODESolveRK.h"

/* time is multiplied by the growth rate of human Gamma_growth,
 * while population is divided by the carrying capacity K'_0.
 * By doing that,
 * we can deal with dimensionless quantities. */

const double t_ini = 0.;  // initial time
const double t_fin = 20.;  // final time
const double delta_t = 0.01;  // size of timestep in RK
// birth rate (divided by growth rate of human)
const double Gamma_birth = 1.;
// death rate of adult (divided by growth rate of human)
const double Gamma_death_ad = 1. / 3.;
// death rate of child (divided by growth rate of human)
const double Gamma_death_ch = 0.;
// time at which the (effective) carrying capacity increases
const double t_add = 5.;
// additional (effective) carrying capacity
const double k_add = 1.;

// time derivative of adult population
double dn_adult_dt(double t, double *n);
// time derivative of child population
double dn_child_dt(double t, double *n);
// (effective) carrying capacity K' divided by its initial value
double K_prime(double t);

int main(int argc, char *argv[]) {
    /* array of function pointer for time derivatives
     * of population */
    func_oderk_deriv *ptr_in_func;
    ptr_in_func =
        (func_oderk_deriv *)malloc(sizeof(func_oderk_deriv) * 2);
    ptr_in_func[0] = &dn_adult_dt;
    ptr_in_func[1] = &dn_child_dt;

    // initial population of adult (N at t_ini)
    double n_adult_ini =
        log(Gamma_birth / Gamma_death_ad) +
        log((1. - Gamma_death_ch) / (1 + Gamma_death_ch));
    // initial population of child (N at t_ini)
    double n_child_ini =
        Gamma_death_ad * n_adult_ini / (1. - Gamma_death_ch);

    /* arrays to store the evolution history
     * of population */
    int nbin_t = (int)floor(fabs(t_fin - t_ini) / delta_t + 1e-8);
    double *t_history;
    std::vector<double> *n_history;
    t_history = new double [nbin_t + 1];
    n_history = new std::vector<double> [nbin_t + 1];

    t_history[0] = t_ini;
    n_history[0].clear();
    n_history[0].push_back(n_adult_ini);
    n_history[0].push_back(n_child_ini);

    ODESolveRK ode_solver;
    // initialize the ODE Runge-Kutta solver
    bool initialized =
        ode_solver.init(2, t_history[0], n_history[0], ptr_in_func);

    int it_max = 0;
    for (int it = 1; it <= nbin_t; it++) {
        bool go_next = ode_solver.next_RK4(delta_t);
        if (!go_next) {
            break;
        }
        it_max += 1;

        ode_solver.get_system_current(t_history[it], n_history[it]);
        fprintf(stderr, "  %e  %e  %e\n", t_history[it],
            n_history[it].at(0), n_history[it].at(1));
    }

    char filename_prefix[200];
    char filename_extend[200];

    bool fname_arg_prefix = argc >= 2;
    if (fname_arg_prefix) {
        strcpy(filename_prefix, argv[2]);
    } else {
        strcpy(filename_prefix, "population_model01");
    }

    bool fname_arg_extend = argc >= 3;
    if (fname_arg_extend) {
        strcpy(filename_extend, argv[2]);
    } else {
        strcpy(filename_extend, "dat");
    }

    char buffer[10];
    sprintf(buffer, "%.1f", k_add);

    FILE *fout;
    char filename_out[200];
    strcpy(filename_out, filename_prefix);
    strcat(filename_out, "_k_add_");
    strcat(filename_out, buffer);
    strcat(filename_out, ".");
    strcat(filename_out, filename_extend);
    fout = fopen(filename_out, "w");
    fprintf(fout, "# N0/K'_0 adult = %e\n", n_adult_ini);
    fprintf(fout, "# N0/K'_0 child = %e\n", n_child_ini);
    fprintf(fout, "# [Gamma_growth t]  [N/K'_0 adult]  [N/K'_0 child]\n");

    for (int it = 0; it <= it_max; it++) {
        fprintf(fout, "  %e  %e  %e\n", t_history[it],
            n_history[it].at(0), n_history[it].at(1));
    }

    fclose(fout);

    delete [] t_history;
    delete [] n_history;
    free(ptr_in_func);

    return 0;
}

double dn_adult_dt(double t, double *n) {
    double ret =
        (1. - Gamma_death_ch) * n[1] - Gamma_death_ad * n[0];
    return ret;
}

double dn_child_dt(double t, double *n) {
    double ret =
        Gamma_birth * n[0] * exp(-n[0] / K_prime(t)) -
        (1. + Gamma_death_ch) * n[1];
    return ret;
}

double K_prime(double t) {
    return 1. + k_add * 0.5 * (1. + tanh(t - t_add));
}

 

성인과 어린이의 인구 수 변화율을 나타내는 함수들이 dn_adult_dt 및 dn_child_dt 로 각각 정의되어 있습니다. 이 함수들은 현재시각 t, 성인 인구 n[0] 및 어린이 인구 n[1] 을 매개변수로 받고 있으며, 시간에 따른 인구 부양력은 K_prime 이라는 함수에 별도로 정의되어 있고요. 그리고 이 함수들의 포인터들을 ODESolveRK 객체에 전달하여 연립 상미분 방정식을 푸는 방식입니다. 인구 부양력에 따라 결정되는 평형상태가 초기조건으로 주어져 있을때, 부양력 K' 가 두배로 증가하면 성인과 어린이의 인구가 어떻게 변화하는지 살펴봅시다.

 

 

인구 부양력이 2배로 증가한 시점에 출산율의 증가로 인해 어린이의 인구가 늘어납니다. 이들이 성장하고 어른이 되면서, 어른의 인구 역시 점진적으로 증가하죠. 어른의 인구는 어린이의 인구에 천천히 증가합니다만, 결과적으로 기존 인구의 2배에 달하는 평형 상태에 도달합니다.

여기서는 인구가 증가하는 시나리오를 살펴보았지만, 인구가 감소하는 상황에 대해서도 비슷한 예상을 할 수 있지 않을까 생각니다. 한국의 저출산 문제처럼 재화의 양이 증가하더라도 사람들의 기대 수준이 그보다 더 높아지면, 실질적 인구 부양력은 감소하게 될 것이고 출산율은 떨어지겠죠. 이렇게 되면 고령화로 인해 젊은 세대의 부담이 늘어나는 것도 문제지만, 장기적으로는 성인의 인구도 감소해서 국가 전체의 경제가 위축되는 문제도 있지 않을까 싶습니다.

 

목차로 ...

 

확장된 가설 : 인간과 삼림

위의 수학 모형을 더 확장해서 삼림을 추가해 보았습니다. 예전에 문명의 붕괴 (재레드 다이아몬드 저)라는 책을 읽은 적이 있는데, 이 책에서는 인간 사회의 멸망이 삼림의 절멸과 밀접한 관련이 있다는 점을 지적하고 있습니다. 남태평양이 여러 섬과 중남미 문명들이 몰락하는 과정에서 공통으로 발견되는 점이라고 하는군요.

 

[독후감] 문명의 붕괴 (by 재레드 다이아몬드)

 

삼림의 벌채로 얻어지는 자원이 인구 부양에 필수적이라는 설정을 반영하여, 나무의 개체 수 N_tree 를 모형에 추가했습니다. 그리고 자연상태에서의 나무 개체 수는 로지스틱 방정식을 따르게 했습니다.

 

 

벌목으로 인한 나무 개체 수의 감소분이 인구 부양력으로 전환되고, 이를 기반으로 출산율이 유지되는 개념을 도입했는데요. 수학모형에서 이를 구현하기 위해 추가적인 상수들이 필요합니다.

 

• 자연적 나무 수 증가율 Gamma_forest
  로지스틱 방정식에서 등장했던 개체 수 증가율과 같은 포지션을 가지고 있습니다. 나무 한 그루가 한번에 맺는 열매의 수와 씨앗이 나무로 성장하기까지 걸리는 시간에 따라 결정되는 양이죠. 여기서는 편의상 나무 한 그루로부터 또 다른 나무 한 그루가 더 번식하기 위해 15년 가량이 걸린다고 가정했습니다. 이 때의 증가율은 1분의 15년입니다.
• 생태계가 부양가능한 최대 나무 수 K_forest
  이것 역시 로지스틱 방정식의 최대 개체 수와 같은 포지션을 차지합니다. 인간이 없는 자연상태에서는 나무의 개체 수가 이 최대값에 수렴합니다만, 인간의 벌목으로 인해 나무의 수는 이보다 적어집니다.
• 나무 한 그루당 인구 부양능력 C_tree
  말 그대로 나무 한 그루에서 얻어진 재화로 몇 명의 사람을 먹여살릴 수 있느냐를 수치화한 것입니다. 숲을 태워서 얻은 양분으로 농사를 짓는 화전이나, 목재로 카누를 만들어 낚시를 하는 것 등 어떤 방식으로 삼림자원을 이용하느냐에 따라 이 값은 달라지게 되는데요. 여기서는 3명으로 가정하겠습니다.
• (성인) 1인당 나무 벌채율 Gamma_log
  성인 1명이 단위시간동안 나무를 얼마나 베어내는지를 나타낸 수치입니다. 이게 높을수록 더 많은 벌목이 이루어진다는 뜻이죠. 그리고 나무의 전체 수가 적어지면 벌채할 수 있는 나무의 수 역시 비례해서 적어지므로, 지수함수가 들어가는 항을 추가해 주었습니다.
• 1인당 재화 소모율 1/tau
  사람들은 살아가면서 식량 등을 포함한 재화를 소모하기 때문에, 자원이 유한하고 추가적인 수급이 없다면 인구 부양력은 감소할텐데요. 인구 부양력이 전체 인구 및 1인당 재화 소모율에 따라 감소하게 해서 이러한 개념을 구현했습니다. 앞서 언급한대로, 재화의 소모를 커버하기 위해서는 나무를 벌목하여 이를 재화로 환산해야 한다는 설정이 있습니다.

 

삼림이 추가된 인구역학 모형을 수치해석으로 다루기 위한 C++ 코드입니다.

test3_population_RK4.cpp [다운로드]

 

#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<math.h>
#include<vector>
#include"ODESolveRK.h"

/* time is multiplied by the growth rate of human Gamma_growth.
 * tree population is divided by K_forest,
 * which is the carrying capacity of forest.
 * Human population is divided by K_forest.
 * By doing that,
 * we can deal with dimensionless quantities. */

const double t_ini = 0.;  // initial time
const double t_fin = 100.;  // final time
const double delta_t = 0.01;  // size of timestep in RK
/* birth rate
 * (divided by growth rate of human) */
const double Gamma_birth = 1.;
/* death rate of adult
 * (divided by growth rate of human) */
const double Gamma_death_ad = 1. / 3.;
/* death rate of child
 * (divided by growth rate of human) */
const double Gamma_death_ch = 0.;
/* growth rate of the population of trees
 * (divided by growth rate of human) */
const double Gamma_forest = 1.;
/* rate at which trees are logged
 * (divided by growth rate of human) */
const double Gamma_log = 1.;
/* how many people can be supported by a single tree
 * This comes into the (effective) human
 * carraying capacity */
const double Cap_tree = 3.;
/* tau times growth rate of human,
 * where tau quantifies how long
 * the (effective) human carrying capacity lasts */
const double tauGamma_growth = 1.;
/* a constant going into the rate,
 * at which trees are logged */
const double slope_log = 1.;

// time derivative of adult population
double dn_adult_dt(double t, double *n);
// time derivative of child population
double dn_child_dt(double t, double *n);
// time derivative of tree population
double dn_tree_dt(double t, double *n);
// time derivative of the (effective) human carrying capacity K'
double dK_prime_dt(double t, double *n);

int main(int argc, char *argv[]) {
    /* array of function pointer for time derivatives
     * of population */
    func_oderk_deriv *ptr_in_func;
    ptr_in_func =
        (func_oderk_deriv *)malloc(sizeof(func_oderk_deriv) * 4);
    ptr_in_func[0] = &dn_adult_dt;
    ptr_in_func[1] = &dn_child_dt;
    ptr_in_func[2] = &dn_tree_dt;
    ptr_in_func[3] = &dK_prime_dt;

    // initial population of adult (at t_ini)
    double n_adult_ini = 0.02;
    // initial population of child (at t_ini)
    double n_child_ini = 0.;
    // initial population of tree (at t_ini)
    double n_tree_ini = 1.;
    // initial (effective) human carrying capacity (K' at t_ini)
    double K_prime_ini = 0.02;

    /* arrays to store the evolution history
     * of population */
    int nbin_t = (int)floor(fabs(t_fin - t_ini) / delta_t + 1e-8);
    double *t_history;
    std::vector<double> *n_history;
    t_history = new double [nbin_t + 1];
    n_history = new std::vector<double> [nbin_t + 1];

    t_history[0] = t_ini;
    n_history[0].clear();
    n_history[0].push_back(n_adult_ini);
    n_history[0].push_back(n_child_ini);
    n_history[0].push_back(n_tree_ini);
    n_history[0].push_back(K_prime_ini);

    ODESolveRK ode_solver;
    // initialize the ODE Runge-Kutta solver
    bool initialized =
        ode_solver.init(4, t_history[0], n_history[0], ptr_in_func);

    int it_max = 0;
    for (int it = 1; it <= nbin_t; it++) {
        bool go_next = ode_solver.next_RK4(delta_t);
        if (!go_next) {
            break;
        }
        it_max += 1;

        ode_solver.get_system_current(t_history[it], n_history[it]);
        fprintf(stderr, "  %e  %e  %e  %e  %e\n", t_history[it],
            n_history[it].at(0), n_history[it].at(1),
            n_history[it].at(2), n_history[it].at(3));
    }

    char filename_prefix[200];
    char filename_extend[200];

    bool fname_arg_prefix = argc >= 2;
    if (fname_arg_prefix) {
        strcpy(filename_prefix, argv[2]);
    } else {
        strcpy(filename_prefix, "population_model02");
    }

    bool fname_arg_extend = argc >= 3;
    if (fname_arg_extend) {
        strcpy(filename_extend, argv[2]);
    } else {
        strcpy(filename_extend, "dat");
    }

    char buffer[10];
    sprintf(buffer, "%.1f", Gamma_log);

    FILE *fout;
    char filename_out[200];
    strcpy(filename_out, filename_prefix);
    strcat(filename_out, "_Gamma_log_");
    strcat(filename_out, buffer);
    strcat(filename_out, ".");
    strcat(filename_out, filename_extend);
    fout = fopen(filename_out, "w");
    fprintf(fout, "# N0_adult / K_forest = %e\n", n_adult_ini);
    fprintf(fout, "# N0_child / K_forest = %e\n", n_child_ini);
    fprintf(fout, "# N0_tree / K_forest = %e\n", n_tree_ini);
    fprintf(fout, "# tauGamma_growth = %e\n", tauGamma_growth);
    fprintf(fout, "# Gamma_log = %e\n", Gamma_log);
    fprintf(fout, "# [Gamma_growth t]");
    fprintf(fout, "  [N_adult / K_forest]");
    fprintf(fout, "  [N_child / K_forest]");
    fprintf(fout, "  [N_tree / K_forest]");
    fprintf(fout, "  [K'(human) / K_forest]\n");

    for (int it = 0; it <= it_max; it++) {
        fprintf(fout, "  %e  %e  %e  %e  %e\n", t_history[it],
            n_history[it].at(0), n_history[it].at(1),
            n_history[it].at(2), n_history[it].at(3));
    }

    fclose(fout);

    delete [] t_history;
    delete [] n_history;
    free(ptr_in_func);

    return 0;
}

double dn_adult_dt(double t, double *n) {
    double ret =
        (1. - Gamma_death_ch) * n[1] - Gamma_death_ad * n[0];
    return ret;
}

double dn_child_dt(double t, double *n) {
    double factor_exp;
    if (n[3] > 1e-6 && fabs(n[0] / n[3]) < 100.) {
        factor_exp = exp(-n[0] / n[3]);
    } else {
        factor_exp = 0.;
    }

    double ret =
        Gamma_birth * n[0] * factor_exp -
        (1. + Gamma_death_ch) * n[1];
    return ret;
}

double dn_tree_dt(double t, double *n) {
    if (n[2] < 1e-6) {
        return 0.;
    }

    double factor_exp = exp(-slope_log * n[2]);
    double ret =
        Gamma_forest * n[2] * (1. - n[2]) -
        Gamma_log * n[0] * (1. - factor_exp);
    return ret;
}

double dK_prime_dt(double t, double *n) {
    double factor_exp = exp(-slope_log * n[2]);
    double ret =
        Cap_tree * Gamma_log * n[0] * (1. - factor_exp) -
        (n[0] + n[1]) / tauGamma_growth;

    if (n[3] <= 0. && ret < 0.) {
        ret = 0.;
    }

    return ret;
}

 

어른과 어린이의 인구변화율 dn_adult_dt 및 dn_child_dt 이외에도, 나무의 개체 수 변화율 dn_tree_dt 와 인구 부양력의 시간 변화율 dK_prime_dt 가 추가되었습니다. 이들은 현재시각 t, 성인 인구 수 n[0], 어린이 인구 수 n[1], 나무 개체 수 n[2], 인구 부양력 n[3] 을 매개변수로 받는 함수들입니다. 결론적으로 4개 함수의 연립 1차 미분방정식을 풀게 되는거죠.

 

수치계산으로 얻어진 첫번째 시나리오입니다.

 

 

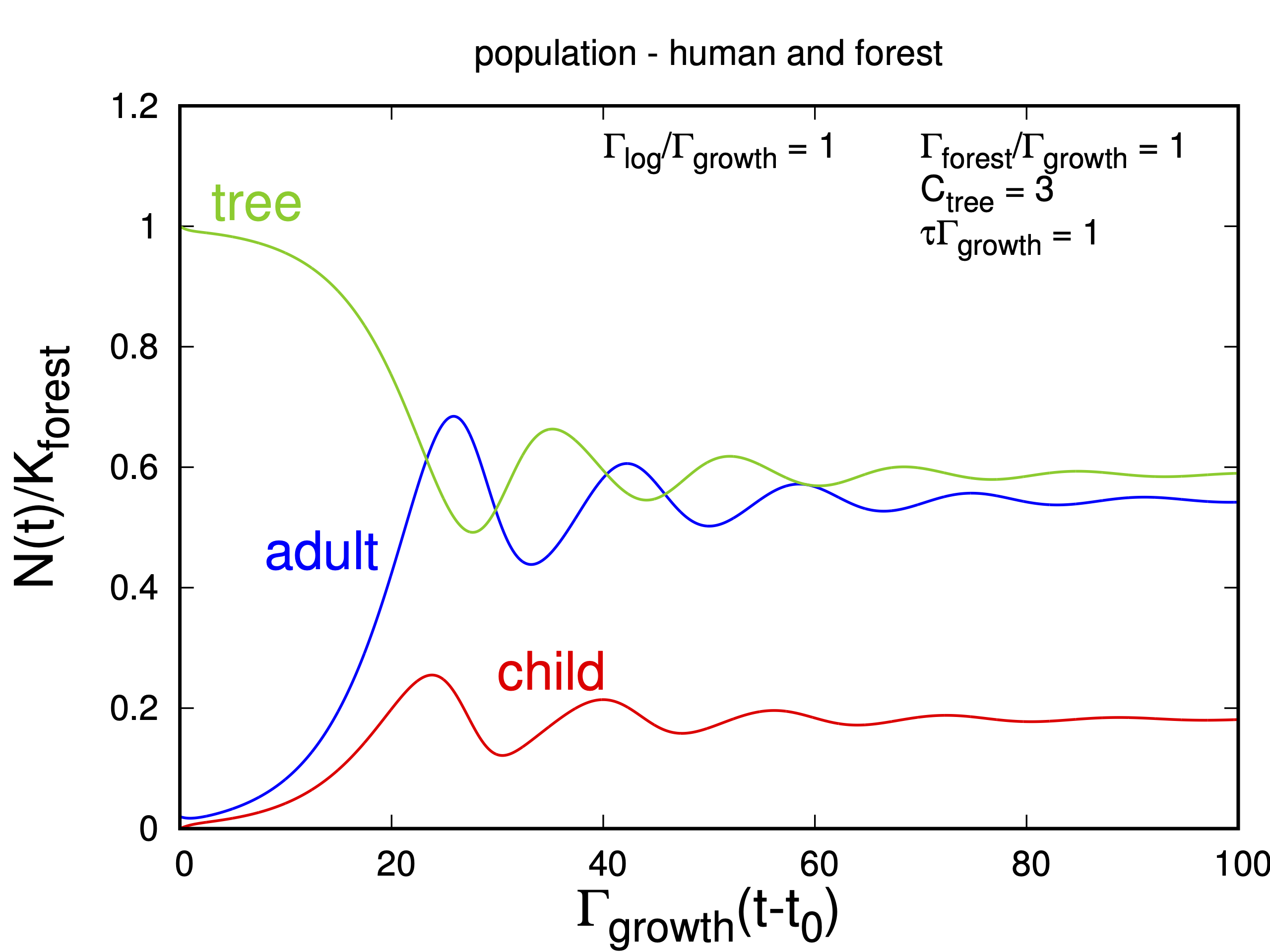
나무의 개체 수가 감소함에 따라, 벌채된 나무들이 인간의 생존에 필요한 재화로 환산되어 인구는 증가하는 것을 볼 수 있습니다. 삼림의 벌채로 인해 나무의 개체 수가 자연상태에서 허용되는 최대값에 비해 적은데요. 그럼에도 불구하고 삼림의 자연적인 재생능력이 벌채로 인한 감소분을 커버할 수 있는 덕택에, 인간과 삼림의 공존이 이루어지는 케이스입니다.

 

이번에는 다른 시나리오를 상정해서 계산을 해 봅시다. 나무를 지나치게 벌채하여 결국 삼림이 절멸하고, 인구를 부양할 수 있는 자원이 소실되어 인간사회 역시 붕괴하는 경우입니다. 앞에 언급된 경우와 비교했을 때 차이점은 삼림 벌채율 Gamma_log 의 값이 높다는 점입니다.

 

 

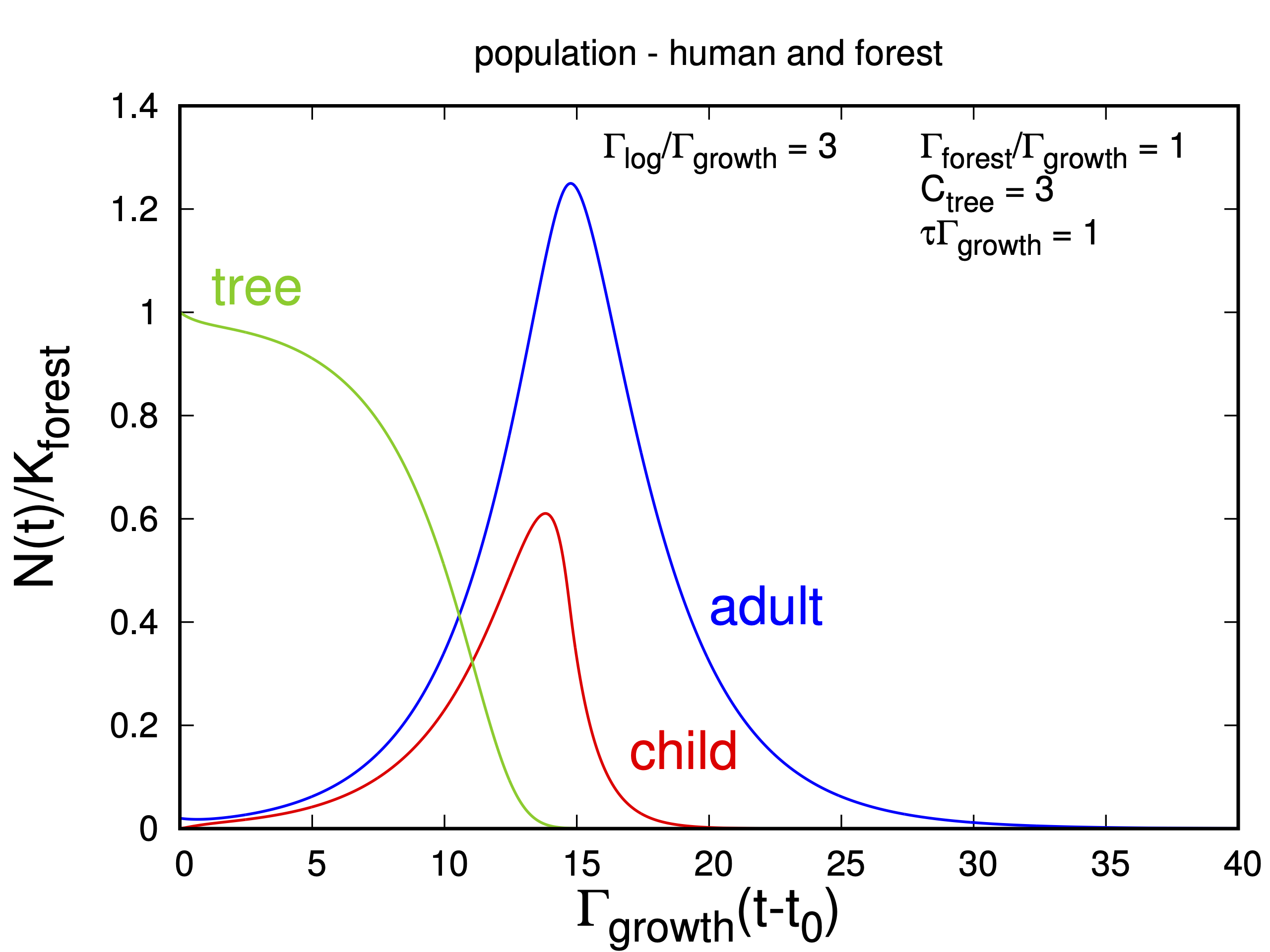
더 많은 나무를 베어냄으로 인해, 가용 자원이 단기간에 증가하고 인구도 폭증하는데요. 인구 수가 절정에 달했을 때는 인간과 삼림이 상생하는 경우보다도 훨씬 많습니다. 하지만 자연적인 삼림 재생능력이 벌채되는 양을 커버하지 못하고 삼림이 절멸하고, 이에 따라 인간사회 역시 소멸하는 운명을 맞이했네요.

 

목차로 ...

 

지금까지 간단한 수학 모형을 통해 다양한 상황에서 인구가 어떻게 변화하는지를 살펴보았습니다. 사실은 말이 안되는 결과가 나와서 중간에 모형을 수정하기도 했는데요. 하지만 결과적으로 단순하면서도 상식과 모순되지 않는 결론을 수치실험으로 얻는 작업은 그 자체로 흥미있는 일이었습니다. 전반적인 과정이 제가 물리학 연구를 할 때랑 비슷한 면도 있고요.

한줄요약 : 삼림을 보호합시다. (뭐야 그게?)

 

---

 

이 포스팅에 나온 C++ 프로그램에서는 미분 방정식을 풀기 위한 방법으로 함수의 포인터를 이용하고 있는데요. 이를 통해 함수 자체를 다른 함수의 매개변수로 넘겨주는 것이 가능하고, 다양한 용도로 활용이 가능합니다. 자세한 사항은 다음 포스팅에 소개되어 있습니다.

 

C/C++ 에서 함수를 매개변수로 사용하기