GSL : C/C++ 수치해석 라이브러리

라이브러리 소개

이번 포스팅에서는 이공계 분야의 수치해석에서 널리 쓰이는 GSL라이브러리에 대해 써 볼까 합니다. GSL은 GNU Scientific Library의 약자로서, 과학 및 공학 분야의 수치해석에 유용한 여러가지 함수들을 가지고 있는 C언어 라이브러리인데요. 어지간한 슈퍼컴퓨터에는 기본적으로 설치되어 있을 정도로 널리 쓰이기 때문에, 기본적인 사용 방법들을 알아두면 상당히 좋습니다.

 

GSL - GNU Scientific Library - GNU Project - Free Software Foundation

 

개인용 컴퓨터에서 사용할 경우에는 먼저 라이브러리를 설치해야 하는데, 리눅스나 유닉스 사용자라면 위에 언급된 웹사이트에서 소스파일을 받아서 라이브러리를 빌드하는것이 가능합니다. macOS 사용자라면, homebrew를 통해서 설치할 수도 있는데요.

 

 

터미널 콘솔에서 brew info gsl 을 입력하면 GSL라이브러리에 대한 정보가 뜨고 brew install gsl 을 입력하여 설치를 할 수 있습니다. 물론 인터넷은 연결되어 있어야겠죠. 설치가 정상적으로 끝났다면, brew list 를 통해 설치된 패키지들을 확인했을 때 gsl이 있을 것입니다.

 

 

윈도우 사용자의 경우, vcpkg를 통해서 라이브러리를 설치하면 비주얼 스튜디오에서 사용할 수 있는데요. 자세한 사항은 다음 포스팅을 참고하면 좋습니다.

 

vcpkg로 비주얼 스튜디오 라이브러리 설치하기

 

라이브러리의 자세한 사용방법은 웹사이트에서 제공하는 온라인 매뉴얼을 참고하면 됩니다. 워낙에 방대한 기능을 가지고 있는지라 이 포스팅 하나에 모두 언급하기는 어렵고, 필요에 따라 해당 기능을 찾아보면서 활용하는 편이 좋습니다. 한가지 주의해야 할 점이 있다면 GSL 라이브러리의 헤더파일들이 include/gsl 서브디렉토리 안에 있다는 것인데요. 헤더파일들을 포함시킬때 include 디렉토리로부터의 상대적인 위치를 명시해야 한다는 점을 감안해야 합니다. 예를 들어서 gsl_math.h 파일을 소스코드에 추가하려면 다음과 같이 합니다.

 

#include<gsl/gsl_math.h>

 

라이브러리를 링크할 때는 -lgsl 및 -lgslcblas 옵션을 추가해줍니다.

 

반응형

 

예시 : 열평형 상태의 페르미 입자

이제 GSL 라이브러리를 이용하여 실용적인 물리 문제를 하나 풀어봅시다. 여기서는 열평형 상태에 있는 상대론적 페르미 입자를 다뤄볼텐데요. 엄밀히 말하면 스핀 각운동량이 1/2의 홀수배가 되는 입자들을 통틀어서 페르미 입자라 부르며, 친숙한 양성자나 전자 등의 입자들이 대표적인 예시입니다. 이러한 입자들이 열평형 상태에 놓이게 될 경우, 특정 위치에서 특정 운동량을 가지게 될 확률은 페르미-디랙 (Fermi-Dirac) 분포를 따르게 되죠.

 

 

이 페르미-디랙 분포함수를 모든 운동량에 대해 적분하면, 단위 부피당 입자들의 평균개수를 구할 수 있습니다. 이 적분은 실제로 해석적인 계산이 가능하며, 그 결과가 제2종 변형 베셀 함수의 형태로 나타나는 것이 특징입니다. 비슷하게 단위 부피당 에너지를 계산할 수 있습니다.

 

 

에너지 밀도를 개수 밀도로 나누면, 입자 한개가 지니고 있는 평균값을 구할 수 있을 것입니다. 그리고 여기서 다시 정지질량 에너지 엠씨스퀘어를 빼면, 운동에너지의 평균값이 나오겠죠. GSL 라이브러리에서 제공되는 1차원 가우스-라게르 (Gauss-Laguerre) 적분을 통해 수치계산을 한 뒤에, 이를 해석적인 값과 비교해 보겠습니다.

 

소스 코드입니다.
test1_FD_gsl.cpp [다운로드]

 

#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<math.h>
#include<gsl/gsl_math.h>
#include<gsl/gsl_sf_bessel.h>
#include<gsl/gsl_integration.h>

struct _particle_system_ {
    /* power for the integrand
     * of the 1-dimensional integration */
    int pow_alpha;
    int degen_spin;  // spin degeneracy
    double mass_scaled;  // mass divided by temperature

    /* number density devided by
     * temperature^3 */
    double nden_scaled_base;
    double nden_scaled_int1;

    /* energy density devided by
     * temperature^4 */
    double eden_scaled_base;
    double eden_scaled_int1;
} typedef specie;

// precision of the series in the analytic calculation
const double eps_precision = 1e-6;

// thermal distribution function
double get_fden_th_scaled(specie &particle_in, double p_scaled);

/* number and energy density of particles in thermal equilibrium
 * in terms of the modified Bessel function (2-nd kind) */
void get_eden_th_scaled_base(specie &particle_in);

/* functions and variables
 * for the 1-dimensional numerical integration
 * using Gauss-Laguerre fixed-point quadratures */
void get_eden_th_scaled_int1(specie &particle_in);
double gsl_func_nden_int1(double p_scaled, void *params);
double gsl_func_eden_int1(double p_scaled, void *params);
gsl_integration_fixed_workspace *work_int1;
const gsl_integration_fixed_type *type_int1 =
    gsl_integration_fixed_laguerre;
int n_nodes_int1 = 32;  // number of nodes

// the main function
int main(int argc, char *argv[]) {

    int nlat_m_scaled = 100;
    double m_scaled_min = 0.01;
    double m_scaled_max = 100.;
    double *lat_m_scaled;
    specie *lat_specie;
    lat_m_scaled = new double [nlat_m_scaled + 1];
    lat_specie = new specie [nlat_m_scaled + 1];
    for (int ilat = 0; ilat <= nlat_m_scaled; ilat++) {
        lat_m_scaled[ilat] = m_scaled_min *
            exp(log(m_scaled_max / m_scaled_min) *
                (double)ilat / (double)nlat_m_scaled);

        lat_specie[ilat].pow_alpha = 2;
        lat_specie[ilat].degen_spin = 2;
        lat_specie[ilat].mass_scaled = lat_m_scaled[ilat];
    }

    char filename_prefix[200];
    char filename_extend[200];

    bool fname_arg_prefix = argc >= 2;
    if (fname_arg_prefix) {
        strcpy(filename_prefix, argv[2]);
    } else {
        strcpy(filename_prefix, "eden_th_FD_scaled");
    }

    bool fname_arg_extend = argc >= 3;
    if (fname_arg_extend) {
        strcpy(filename_extend, argv[2]);
    } else {
        strcpy(filename_extend, "dat");
    }


    FILE *fout_base;
    char filename_base[200];
    strcpy(filename_base, filename_prefix);
    strcat(filename_base, "_base.");
    strcat(filename_base, filename_extend);
    fout_base = fopen(filename_base, "w");
    fprintf(fout_base, "# mass_over_T\n");
    fprintf(fout_base, "#   eden_over_T_pow4\n");
    fprintf(fout_base, "#     nden_over_T_pow3\n");
    fprintf(fout_base, "#       kinetic_energy_per_particle_over_T\n");

    FILE *fout_int1;
    char filename_int1[200];
    strcpy(filename_int1, filename_prefix);
    strcat(filename_int1, "_int1.");
    strcat(filename_int1, filename_extend);
    fout_int1 = fopen(filename_int1, "w");
    fprintf(fout_int1, "# mass_over_T\n");
    fprintf(fout_int1, "#   eden_over_T_pow4\n");
    fprintf(fout_int1, "#     nden_over_T_pow3\n");
    fprintf(fout_int1, "#       kinetic_energy_per_particle_over_T\n");

    work_int1 =
        gsl_integration_fixed_alloc(type_int1, n_nodes_int1, 0., 1., 0., 0.);

    for (int ilat = 0; ilat <= nlat_m_scaled; ilat++) {
        get_eden_th_scaled_base(lat_specie[ilat]);
        get_eden_th_scaled_int1(lat_specie[ilat]);

        double ergkin_per_particle_base =
            lat_specie[ilat].eden_scaled_base /
            lat_specie[ilat].nden_scaled_base -
            lat_m_scaled[ilat];
        double ergkin_per_particle_int1 =
            lat_specie[ilat].eden_scaled_int1 /
            lat_specie[ilat].nden_scaled_int1 -
            lat_m_scaled[ilat];

        fprintf(fout_base, "  %e  %e  %e  %e\n",
            lat_m_scaled[ilat],
            lat_specie[ilat].eden_scaled_base,
            lat_specie[ilat].nden_scaled_base,
            ergkin_per_particle_base);
        if ((ilat + 2) % 5 == 0) {
            fprintf(fout_int1, "  %e  %e  %e  %e\n",
                lat_m_scaled[ilat],
                lat_specie[ilat].eden_scaled_int1,
                lat_specie[ilat].nden_scaled_int1,
                ergkin_per_particle_int1);
        }
    }

    gsl_integration_fixed_free(work_int1);


    fclose(fout_base);
    fclose(fout_int1);

    delete [] lat_m_scaled;
    delete [] lat_specie;

    return 0;
}

double get_fden_th_scaled(specie &particle_in, double p_scaled) {
    int a_stat;
    double ad;
    if (particle_in.degen_spin == 0) {
        a_stat = 0;
    } else {
        if (particle_in.degen_spin % 2 == 1) {
            a_stat = 1;  // boson
        } else {
            a_stat = -1;  // fermion
        }
    }
    ad = (double)a_stat;

    double m_scaled = particle_in.mass_scaled;

    double e_scaled =
        sqrt(p_scaled * p_scaled + m_scaled * m_scaled);
    return 1. / (8. * M_PI * M_PI * M_PI * (exp(e_scaled) - ad));
}

void get_eden_th_scaled_base(specie &particle_in) {
    int a_stat;
    double ad;
    if (particle_in.degen_spin == 0) {
        a_stat = 0;
    } else {
        if (particle_in.degen_spin % 2 == 1) {
            a_stat = 1;  // boson
        } else {
            a_stat = -1;  // fermion
        }
    }
    ad = (double)a_stat;

    double m_scaled = particle_in.mass_scaled;

    int l = 0;
    double sign = 1.;
    double nden_now = 0.;
    double eden_now = 0.;
    bool converging = false;
    do {
        l += 1;
        double ld = (double)l;

        if (l > 1) {
            sign = sign * ad;
        }

        double nden_prev = nden_now;
        double eden_prev = eden_now;

        nden_now += sign * gsl_sf_bessel_Kn(2, ld * m_scaled) / ld;
        eden_now += sign *
            (3. * gsl_sf_bessel_Kn(2, ld * m_scaled) / (ld * ld) +
            m_scaled * gsl_sf_bessel_Kn(1, ld * m_scaled) / ld);

        converging =
            fabs(nden_now - nden_prev) < fabs(nden_now) * eps_precision &&
            fabs(eden_now - eden_prev) < fabs(eden_now) * eps_precision;
    } while (!converging);

    nden_now = nden_now * m_scaled * m_scaled / (2. * M_PI * M_PI);
    eden_now = eden_now * m_scaled * m_scaled / (2. * M_PI * M_PI);

    particle_in.nden_scaled_base = nden_now;
    particle_in.eden_scaled_base = eden_now;

    return;
}

void get_eden_th_scaled_int1(specie &particle_in) {
    specie part = particle_in;
    part.pow_alpha = 2;

    int inegrated = 0;

    double nden_int1 = 0.;
    gsl_function F_nden;
    F_nden.function = &gsl_func_nden_int1;
    F_nden.params = &part;
    inegrated = gsl_integration_fixed(&F_nden, &nden_int1, work_int1);
    particle_in.nden_scaled_int1 = nden_int1;

    double eden_int1 = 0.;
    gsl_function F_eden;
    F_eden.function = &gsl_func_eden_int1;
    F_eden.params = &part;
    inegrated = gsl_integration_fixed(&F_eden, &eden_int1, work_int1);
    particle_in.eden_scaled_int1 = eden_int1;

    return;
}

double gsl_func_nden_int1(double p_scaled, void *params) {
    specie part = *(specie *)params;
    int alpha = part.pow_alpha;

    double f = 4. * M_PI * gsl_pow_int(p_scaled, alpha) *
        exp(p_scaled) * get_fden_th_scaled(part, p_scaled);
    return f;
}

double gsl_func_eden_int1(double p_scaled, void *params) {
    specie part = *(specie *)params;
    int alpha = part.pow_alpha;

    double m_scaled = part.mass_scaled;

    double e_scaled =
        sqrt(p_scaled * p_scaled + m_scaled * m_scaled);

    double f = 4. * M_PI * gsl_pow_int(p_scaled, alpha) * e_scaled *
        exp(p_scaled) * get_fden_th_scaled(part, p_scaled);
    return f;
}

 

원주율은 M_PI 라는 이름으로 정의되어 있고, 이를 사용하기 위해서 gsl_math.h 헤더파일을 포함시켰습니다. 앞서 언급한 대로 해석적인 계산을 위해서는 베셀 함수를 사용해야 하고, 제 2종 변형 베셀 함수는 GSL 라이브러리 내에서 gsl_sf_bessel_Kn 라는 이름을 가지고 있는데요. 이를 사용하려면 gsl_sf_bessel.h 헤더파일이 필요합니다. 마지막으로 1차원 정적분을 위해서는 gsl_integration.h 헤더파일을 포함시켜야 합니다. 계산을 위해서는 gsl_integration_fixed_alloc, gsl_integration_fixed, gsl_integration_fixed_free 등의 함수를 호출해야 하고, 적분 대상이 되는 함수의 포인터를 GSL 라이브러리에 넘겨주는 형식을 취하고 있습니다.

 

그리하여 프로그램을 돌려보면, 수치적분으로 도출된 값들이 해석적인 결과와 잘 일치한다는 걸 볼 수 있죠.

 

 

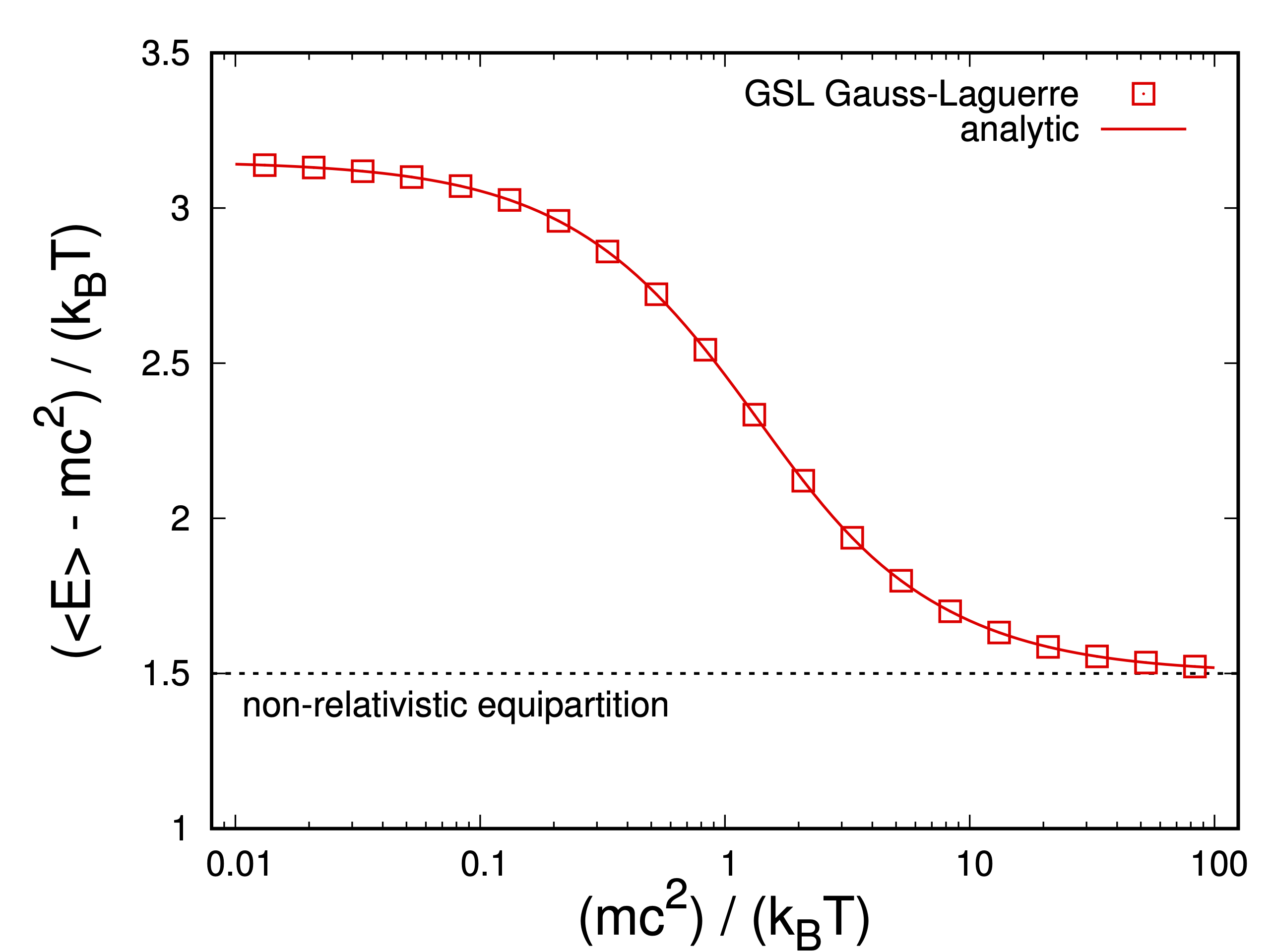
온도 대비 질량에 따라 평균 운동에너지가 어떻게 달라지는지를 볼 수 있는데요. 한가지 눈여겨볼 것은 입자 하나의 정지질량 에너지가 온도에 비해 매우 크다면, 운동에너지는 온도의 1.5배로 수렴한다는 것입니다. 이것은 운동에너지가 정지질량 에너지에 비해 매우 작은 비상대론적 케이스에 해당되고, 고등학교 물리2 또는 대학교 일반물리에 등장하는 에너지 등분배법칙에 부합하는 결과라 할 수 있죠.

 

---

 

앞서 함수의 포인터에 대해 언급을 했었는데, 이것을 이용하면 함수 자체를 또다른 함수의 매개변수로 넘겨주는 것도 가능합니다. 자세한 것은 아래의 포스팅에 소개되어 있습니다.

 

C/C++ 에서 함수를 매개변수로 사용하기

 

그리고 메인 함수는 argc 및 argv 라는 매개변수들을 가지고 있는데요. 이들은 명령행 인자 (command-line arguments)라고 불리는 것들로서, 여기서는 출력파일의 이름과 확장자를 지정하는 목적으로 사용되고 있습니다. C언어 및 C++ 의 명령행 인자에 대한 자세한 사항은 아래의 포스팅에 소개되어 있습니다.

 

Command-line arguments (C/C++ 명령행 인자)

 

---

 

위의 예시에 나온 그래프는 GNUPLOT (그누플롯)이라는 프로그램을 이용해서 그렸습니다. 이 무료 프로그램을 이용하면 다양한 형태의 그래프를 그릴 수 있어서 유용하죠. 자세한 사항은 다음 포스팅에 소개되어 있습니다.

 

GNUPLOT : 다용도 그래프 유틸리티